Liceo Scientifico
V. ROMANO Piazza Armerina
Classe I-A
Prof. Lina Carini
Classe III-B
Prof. Carmela Buscemi
La Consegna:
La seguente affermazione è sempre vera?
Un numero pari si può sempre scomporre nella
somma di due primi?
Argomentare le vostre affermazioni.
Tempo per la consegna: 2 ore.
Organizzazione
del lavoro:
- Fase 1: riflessione individuale sul quesito
proposto (tempo 1 ora)
- Fase 2: argomentare in assetto di piccolo gruppo e
registrazione delle strategie individuali (tempo un ora)
Analisi a priori della prima
fase
A1:
Verifica la congettura sommando numeri primi progressivi e verificando se la
somma è pari oppure no.
A2:
Sceglie un numero pari e considera i numeri primi inferiori ad esso; quindi
verifica la congettura scegliendo uno di questi numeri primi e constatando se
il complementare (differenza tra il pari e il primo considerato) è anchesso
primo.(uso delle tavole).
A3:
Scompone il numero pari come somma di unità; quindi applica la proprietà
associativa fino ad ottenere due primi tali che la somma sia il numero
considerato.
A4:
Scompone il numero pari in fattori primi e somma i fattori cercando di ottenere
due primi.
A5:
Verifica la congettura considerando numeri primi presi a caso.
A6: Si
basa sulle cifre finali di un numero primo per accertare la verità
dellaffermazione.
A7:
Verifica se il numero pari è scomponibile nel prodotto di due primi più un
altro primo.
A8:
Verifica la congettura prendendo numeri naturali pari a caso oppure consecutivi.
A9:
Verifica la congettura basandosi sulla conoscenza che la somma di due numeri
dispari è sempre un numero pari e
osservata la particolarità del numero due, conclude che la congettura è vera
per numeri pari maggiori di due.
ANALISI QUALITATIVA
Gli alunni della Secondaria Superiore
hanno affrontato la consegna con piena consapevolezza del contenuto, in quanto
già conoscono i numeri primi, i numeri pari, i numeri dispari e i criteri di
divisibilità.
(tempo: 1 ora)
Nella prima ora gli alunni
affrontano la consegna in modo individuale .
Ognuno di loro con più o meno difficoltà cerca di
dimostrare la congettura
utilizzando la tavola dei numeri primi e
in qualche caso la calcolatrice.
(tempo: 1 ora)
Gli allievi si dividono in sei gruppi e in ogni gruppo
ciascuno di loro socializza ai compagni la propria strategia.
Ogni gruppo socializza agli altri la
propria strategia cercando di farla emergere.
In
tutti i protocolli è presente laspetto pragmatico, nellapproccio alla
consegna. Dallanalisi emerge che la maggior parte degli alunni ha cercato di provare la congettura di Goldbach
seguendo un procedimento
dimostrativo di tipo induttivo (classe 1a),
Gli allievi verificano la congettura analizzando numeri pari
piccoli in successione e numeri pari grandi presi a caso: alla luce dei
risultati si rileva che il procedimento dimostrativo è prettamente induttivo,
come già detto.
In questa fase la maggior parte degli alunni ha considerato
anche il numero uno come numero primo,
perché, in caso contrario, essi hanno sostenuto che la congettura potrebbe
rivelarsi. non attendibile
Superata lincertezza tutti gli allievi hanno individuato
la condizione che per verificare la congettura di Goldbach si debba partire da
numeri pari maggiori del numero 2.
Inoltre, dato che il numero due è lunico numero primo
pari, si è notato che la scomposizione del numero pari quattro è anche un caso
particolare, perché è lunico scomponibile nella somma di due numeri primi
pari: 4 = 2 + 2.
Alcuni
hanno tentato di verificare la
congettura con un metodo
sperimentale:
Alcuni
allievi hanno cercato di procedere in modo ipotetico-deduttivo:
Per
esempio, un allievo formula le seguenti
ipotesi:
1a
Ipotesi: si può scomporre un numero
pari nella somma di due numeri primi considerando le due metà del numero dato:
2
= 1+1; 4 = 2+2; 6 = 3+3; 8 = 4+4;
e
fa altre prove
, ma trovato un controesempio considera una 2a Ipotesi:
cerca un altro modo per scomporre i numeri pari , che nelle precedenti prove
non era riuscito a scomporre nella somma di due primi e trova che è possibile
scomporre tali numeri pari nella somma di un numero primo ,immediatamente
precedente, con il 3 oppure con 5 oppure con 7; concludendo:
Secondo me un numero pari è sempre
scomponibile nella somma di due numeri primi, perché la differenza tra
un pari e un primo , dà come risultato un numero primo.
Come
si può notare cè un indicatore di generalità denominato sempre e
lindicatore linguistico denominato
perché.
L ipotesi di scomporre un numero pari nella somma di due
numeri primi uguali alla sua metà si riscontra anche in parecchi alunni.
E da rilevare la considerazione che alcuni allievi avendo
trovato il contro esempio del
2 uguale 1+1 (contro esempio di tipo
ostensivo), ritengono che ciò è sufficiente per smentire laffermazione, deducono
quindi che la congettura non è sempre vera; mentre altri concludono che la
congettura di Goldbach è vera per numeri pari maggiori di 2, cioè introducono
una condizione.
E da notare che non ci sono state argomentazioni di tipo
tautologico, in quanto in ogni protocollo è sempre presente la verifica per
più numeri, con opportuna giustificazione.
Per molti allievi largomentazione è stata bloccata dal misconcetto che la somma di numeri dispari da sempre
un numero pari ( Sapere matematico , teorie ingenue ),ed essendo tutti i numeri
primi dispari , ad eccezione del 2, hanno concluso che la congettura è sempre
verificata per tutti i numeri pari > di 2, ed hanno notato anche la
particolare scomposizione del 4 = 2 + 2, cioè il 4 è lunico numero pari che
risulta scomponibile nella somma di due numeri primi pari, essendo il 2 lunico
numero primo pari.
VALIDAZIONE
In alcuni allievi cè il tentativo di trovare un metodo generale per la scomposizione di un qualsiasi numero pari nella somma di due primi.
Per esempio, nel protocollo di un allievo si legge:
Si sa che la somma di due numeri dispari è sempre pari.
Considerando che, ad eccezione del 2,
tutti i numeri primi sono dispari, allora la congettura di Goldbach per essere sempre vera i due numeri
primi devono essere o entrambi diversi da 2 o entrambi uguali a 2.
In formula : p1+p2=
n pari
(con p1=
n primo, p2 = n primo e n numero pari )
se p1 e p2 = 2 , o p1 e p2 diversi da 2 ,
Es. 598 = 587 + 11 ; 4 = 2 + 2.
Qui si riscontra anche un indicatore di condizionalità.
Da un altro protocollo si legge:
Un numero pari ,
si può sempre scomporre nella somma di due numeri primi : 10 =7 + 3; 12 = 7 +
5;14 = 7 + 7;16 = 11 + 5;18 =11 + 7;20 = 13 + 7;
e fa altre prove.
Si può notare che
usando un numero primo come costante e sommando con numeri primi sequenziali
, ma non superiori a 7 si
otterranno sempre numeri pari sequenziali.
E evidente in questo caso che lallievo si trova nellimpossibilità di
estendere la sua sperimentazione allintero insieme N; cè, quindi, una
chiara limitazione del suo processo induttivo.
Ancora da un altro protocollo:
Quindi alla luce delle prove fatte risulta che
la congettura di Goldbach è vera per numeri piccoli , non sembra
tuttavia possibile trovare una regola ,che permetta di scomporre un numero pari
maggiore di 2 nella somma di due numeri primi. Dato che i numeri sono infiniti
e non si possono fare infinite prove,
non si può dimostrare , almeno in questo modo.
Qualche allievo segue il procedimento del metodo di Cantor, cioè preso un numero
pari, sceglie il numero primo più vicino al pari considerato purché sia minore , e calcola la
differenza, se tale differenza è un numero primo, allora il numero pari è
scomponibile nella somma del numero primo che lo precede e il numero primo
ottenuto dalla differenza; se invece, tale differenza non è un numero
primo ripete il procedimento con il
numero primo inferiore, e così via fino a determinare una differenza che
risulti un numero primo, così facendo
si potrà sempre scomporre un numero pari nella somma di due numeri primi.
Alcuni hanno frainteso il tentativo di dimostrazione con la
verifica del caso inverso della congettura di Goldbach; come si evince dalla
seguente annotazione di un allievo:
La congettura di Goldbach è esatta, perché la somma di due
numeri primi, purché dispari(quindi escluso il 2) dà come risultato sempre un
numero pari.
Es: 10 = 5 + 5; 28 = 23 + 5; 64 = 41 + 23.
Ma nel calcolo di
numeri grandi, per facilitare loperazione, abbiamo adottato un metodo, che
consiste :
a) Cercare il numero primo più vicino al numero pari da
scomporre, ricordando che il
numero primo
debba essere sempre minore del numero dato.
b) Trovare la differenza fra il numero pari e il numero
primo scelto.
c) Verificare che la somma fra il numero primo scelto e il
numero primo trovato dalla
differenza del numero pari per il numero dispari primo, dia come risultato
il numero pari scelto.
Es: 1112 = 1109 + 3
; 178 = 161 +17 ; 582 = 563 +
19.
Dallanalisi effettuata si evince che gli indicatori linguistici più comunemente usati sono:
- Sommando vediamo che si formano numeri pari , quindi la congettura di Goldbach è sempre vera .
- Abbiamo notato che
- Inoltre abbiamo verificato che
- Abbiamo altresì notato
- Abbiamo perciò constatato
- Dato che i numeri sono infiniti
- Pertanto
- Quindi Alla luce delle prove fatte risulta che . Non sembra tuttavia possibile
- Quindi
- Si perché
- In quanto..
- perché
- sempre
-Essendo
-Perché essendo .dà sempre
-Considerando le due tabelle (di tipo locale) dove mentre noteremo che contiene sempre
-Può essere sempre vera soltanto se , però può anche essere vera se (indicatore di condizionalità) e ciò è possibile solo
-Discutendo abbiamo dedotto che
-perché dovrebbe
-Quindi essendo
-Noi sappiamo che quindi abbiamo dedotto che dà sempre
-Da questo ne deduciamo che (indicatore di generalità)
Quindi (indicatore di conseguenzialità) affermiamo che si può sempre
-Sapendo che
Si trova anche lindicatore linguistico di generalità sempre.
Cè da sottolineare, infine, che durante la prima fase il docente ha sollecitato gli allievi a rileggere il testo della consegna, per cercare di provare la congettura.
Ogni allievo nella prima fase ha elaborato un protocollo individuale.
Invece, nella seconda fase gli allievi sono stati sollecitati a cercare di formulare un metodo generale per scomporre un qualsiasi numero pari.
Alla fine della seconda fase, per ogni gruppo, un allievo ha socializzato agli altri gruppi la strategia di gruppo, che è stata consegnata in un protocollo, come relazione di gruppo.
Analisi quantitativa cumulativa dei dati
1) Albero implicativo
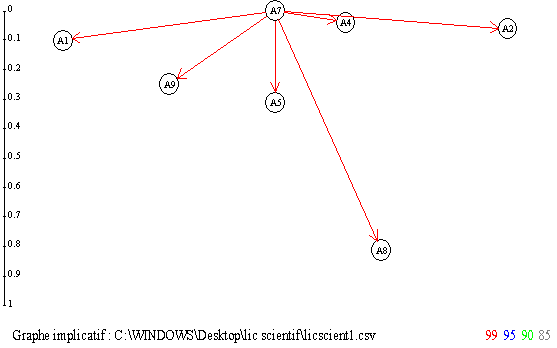
Dal trattamento statistico dei
dati emerge che le concezioni A7 e A4 sono prerequisiti per le altre strategie
utilizzate dagli allievi. Secondo la strategia A7 se lalunno è in grado di
verificare se un numero pari è scomponibile nel prodotto di due primi più un altro primo allora è in grado di
implementare le altre strategie, in particolare anche la strategia A4 secondo
la quale lalunno scompone il numero pari in fattori primi e somma i fattori
cercando di ottenere due primi .
Osserviamo
che la strategia A7 implica tutte le altre in quanto è il teorema di Chen
Jing-Run (1966) secondo il quale un numero pari si può esprimere come somma di
un primo e il prodotto di due primi. Questa è la strategia vincente per la
soluzione della congettura di Goldbach. Naturalmente questo teorema non risolve la congettura ma è strategia che più
si avvicina alla probabile soluzione, e sulla quale i matematici stanno lavorando.
A4 è una strategia simile alla strategia A7 in quanto entrambe si basano sulla
scomposizione di un numero pari in fattori primi
2) Albero della similarità:
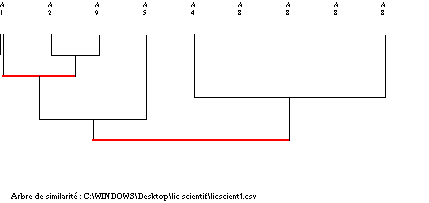
Nella
similarità si evince un legame tra la strategia A2 secondo la quale lalunno sceglie
un numero pari e considera i numeri primi inferiori ad esso; quindi verifica la
congettura scegliendo uno di questi numeri primi e costatando se il complementare (differenza tra il pari
ed il primo considerato) è anchesso primo e la strategia A9 secondo la quale
la somma di due numeri è sempre un numero pari, ma osservata la particolarità
del numero 2, conclude che la congettura è vera per numeri pari maggiori di
due. Tale legame è giustificabile dal misconcetto posseduto dagli alunni
riguardante la somiglianza tra i numeri dispari e i numeri primi. Nei
protocolli si leggono affermazioni del tipo: Si sa che la somma di due numeri dispari è sempre pari. Quindi
considerando che ad eccezione del due
tutti i numeri primi sono dispari, allora la congettura di Goldbach è
sempre vera se i due numeri primi sono entrambi diversi o uguali a due.
La strategia
A1, secondo la quale lalunno verifica la congettura sommando numeri primi
progressivi e verificando cosi se la somma è pari o no, è legata alle strategie
A2 e A9.
La strategia
A1 è collegabile alla strategia A8 infatti sono strategie inverse. Anche le
strategie A2 e A8 sono simili in quanto mentre in A2 lalunno scompone il
numero pari in un numero primo e il suo complementare primo nella strategia A8
lo scompone a caso senza stabilire un criterio.
Anche la
strategie A9 ed A5 sono simili alla strategia A8.
Osserviamo
inoltre che le strategie A1, A2, A5,
A8, A9 sono tra loro indipendenti. Dal trattamento statistico dei dati non è
emerso nessun legame implicativi tra loro.
3) Albero
gerarchico:
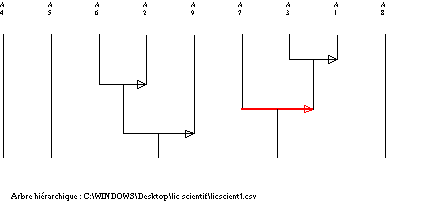
Dal grafo si
evidenzia una gerarchia marcata tra le strategie A3-A1 e A6-A2, ed inoltre la
strategia A7 implica (come già osservato nellanalisi del grafico implicativo)
le strategie A3 ed A1. Le strategie A6-A2 implicano la strategia A9. Le
strategie A4, A5, A9 risultano staccate tra loro e rispetto alle altre
strategie.
ANALISI FATTORIALE
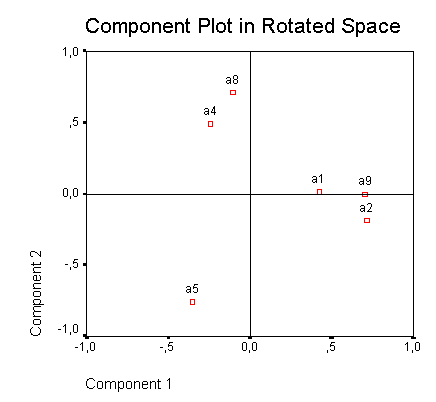
Le strategie
A1, A9 e A2 identificano i fattori lungo lasse orizzontale. Le strategie A4,
A8 sono strategie opposte alla strategia A5 rispetto alle suddette strategie.
Osserviamo che ciò è in perfetto accordo con lalbero della similarità. Le
strategie A4 e A8 sono entrambe strategie sequenziali, e si oppongono alla
strategia A5 in quanto essa non è del tipo sequenziale ma di tipo random.