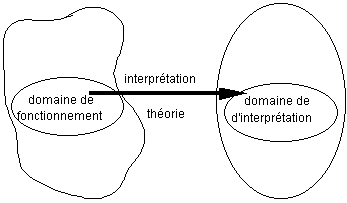
III. Cadre théorique et problématique de la recherche

Nous rappelons que nous avons adopté la définition de la démonstration donnée par Balacheff (1988): “ Il s'agit d'une suite d'énoncés organisée suivant des règles déterminées: un énoncé est connu comme étant vrai ou bien est déduit à partir de ceux qui le précèdent à l'aide d'une règle de déduction prise dans un ensemble de règles bien défini... Ce qui caractérise les démonstrations comme genre de discours est leur forme strictement codifiée ”.

III.1 Cadre théorique

Dans cette partie, nous présentons les points de vue de certains travaux sur les notions de “ Texte mathématique ”, “ Dessin et figure ”, “ Organisation déductive de la démonstration ” et “ Heuristique ”. Nos lectures sur ces notions nous ont orienté pour introduire quatre pôles, fondamentaux dans ce travail de recherche, qui nous ont semblé intéressant à prendre en considération dans l’étude d’une démonstration rédigée par l’élève et que nous désignons par les termes suivants:

Ces quatre pôles seront introduits et définis, progressivement, dans ce cadre théorique. Nous nous appuierons sur ces pôles dans l’étude des phénomènes d’apprentissage et d’enseignement de la démonstration en géométrie, en Tunisie.

Par ailleurs, de nombreux concepts de didactique, soutenant cette recherche, tels que “ Contrat didactique ”, “ Transposition didactique ” etc. ne seront pas repris dans le cadre théorique, car nous estimons que les définitions correspondantes sont suffisamment connues et n’ont pas besoin d’être explicitées (Brousseau, 1986; Chevallard, 1985; Johsua et Dupin, 1993...).

III.1.1 Le texte mathématique

Comme a pu le remarquer Rasolofoniaina (1983) s’inspirant de Glaeser (1976), un texte mathématique présente deux caractéristiques essentielles:

- Les énoncés mathématiques y ont un statut différencié et la prise en compte de ce statut est essentielle pour la compréhension de ce texte.

- Son contenu informationnel est totalement indépendant du code dans lequel il est exprimé: ce dernier peut être soit un langage naturel écrit soit un langage symbolique ou encore un usage mixte des deux.

Notre recherche sur l’enseignement de la démonstration en Tunisie s’intéresse à des textes mathématiques formulés en français qui n’est pas la langue naturelle dans ce pays. De ce fait, une première difficulté des élèves est liée à la connaissance du lexique français, nécessaire pour aborder l’apprentissage des mathématiques. Dans ce travail de recherche, nous ne nous intéresserons pas à cette difficulté, bien qu’elle puisse intervenir dans la lecture et l’écriture des textes de démonstration, cela pouvant faire l’objet d’une perspective de recherche intéressante.

D’autre part, l’utilisation de l’écriture symbolique nécessite une connaissance de son lexique et sa syntaxe. Dans cette écriture, les phrases sont formées par des combinaisons de lettres et de symboles et la difficulté de les écrire (ou de les comprendre) peut dépendre de la longueur des combinaisons ou des conventions implicites utilisées dans ces combinaisons. Par ailleurs, le langage symbolique est concis et précis et présente une économie non négligeable du discours de communication (Glaeser, 1977). La syntaxe dans le langage symbolique n’est pas uniquement un simple codage des phrases naturelles avec des symboles particuliers, mais comme le précise Z. Krygowska (1969): “ Le caractère le plus profond de ce langage, c’est son style, sa construction de phrase qui souvent diffère du style du langage commun ainsi que du langage utilisé dans les autres disciplines enseignées à l’école ”. 

Dans un texte mathématique, les deux types de langage sont souvent imbriqués et l’une des difficultés contenues dans ce texte est le glissement incessant d’un type de langage à un autre.

Ces caractéristiques du texte mathématique nous amènent à prendre en compte différents éléments qui peuvent intervenir dans l’écriture d’une démonstration par l’élève. Il s'agit de voir si les textes produits par les élèves correspondent à une rédaction mathématiquement acceptable. Nous introduisons ainsi le premier pôle dans l’étude que nous entreprenons sur la démonstration, la formulation mathématique, pour lequel nous nous proposons d’étudier cinq éléments différents, intervenant dans l'écriture d'une démonstration, en particulier par les élèves. Ces éléments sont retenus parce qu’ils peuvent représenter des points d’achoppement pour ces derniers. Les deux premiers font l’objet d’un enseignement explicite, alors que les trois autres, concernant l'expression de l'élève pour formuler ses idées, peuvent ne pas être explicités par l’enseignant de mathématiques.

* La notation mathématique c'est-à-dire la désignation des objets mathématiques et de leurs relations mutuelles par des lettres et des symboles (écriture symbolique).

* Les termes mathématiques c'est-à-dire la désignation des objets mathématiques et de leurs relations mutuelles par des termes appartenant au champ lexical mathématique.

En plus de la notation et des termes mathématiques dont l’enseignement relève, normalement, de l’unique responsabilité du professeur de mathématiques, nous nous intéressons à trois autres éléments, intervenant dans la formulation mathématique, qui peuvent être rencontrés dans l’enseignement d’autres disciplines.

* D'abord, une rédaction comportant des expressions marquant le statut propre de chaque énoncé (Duval et Egret, 1989), ce qui permet de distinguer les différents pas de démonstration. Nous estimons qu’au niveau de la 4ème (3ème française), l’élève ne se trompe pas dans l’usage des connecteurs relativement au statut opératoire[1] de chaque énoncé. Ainsi, il serait capable de distinguer ceux désignant les prémisses de ceux consacrés à la conclusion. Cependant, il risque de ne pas les employer dans une démonstration, c’est ce que nous rechercherons..

* Ensuite, une rédaction uniforme où il n'y a pas de mélange non accepté en mathématiques entre écriture symbolique et écriture non symbolique, c'est-à-dire où l'élève respecte les règles d'imbrication de l'écriture symbolique et de la langue française.

* Enfin, l'usage adéquat des anaphores (il, elle, celui-là...). Ce point de la formulation mathématique semble important à étudier dans la mesure où, l'on constate que, certains élèves, surtout dans les petites classes, désignent les objets qu'ils utilisent sans préciser leur nom mais en employant des anaphores, en pensant que le lecteur comprend, de toute évidence, de quoi il s'agit.

Nous signalons que nous avons exclu, de notre recherche, l’étude des éléments qui relèvent uniquement de la formulation en français (orthographe, emploi des temps, vocabulaire français non mathématique...), car nous ne visons pas à rechercher, chez les élèves tunisiens, leur capacité à s’exprimer selon les règles du français.

III.1.2 Le dessin et la figure

Le modèle géométrique a deux caractéristiques: le recours à l'évidence sensible (le dessin joue un rôle fondamental dans la manipulation et dans les évidences sensibles qu'il permet) et la généralité implicite (le procédé de solution ne dépend pas du choix qu'on fait du dessin). Ces caractéristiques sont à l'œuvre dans l’enseignement. Plusieurs travaux en didactique des mathématiques, s’appuyant sur ces deux caractéristiques du modèle géométrique, se sont consacrées à distinguer entre “ Dessin ” et “ Figure ”.

Arsac (1989 a) propose une distinction entre dessin et figure en opposant “ le monde sensible ” et “ le monde géométrique ”:

“ Nous distinguerons dans la suite le dessin et la figure, désignant par dessin le dessin concrètement tracé sur une feuille de papier (ou dans le sable pour Archimède) et par figure l’objet mathématique dont le dessin n’est qu’une représentation... Ainsi, la figure est un élément du monde mathématique et non du monde sensible ”. Cette définition correspond au point de vue des géomètres grecs.

En se plaçant dans le triangle, “ référent, signifiant, signifi頔, Laborde et Capponi (1994) proposent une distinction entre dessin et figure:

“ En tant qu’entité matérielle sur un support, le dessin peut être considéré comme un signifiant d’un référent théorique (objet d’une théorie géométrique comme celle de la géométrie euclidienne, ou de la géométrie projective). La figure géométrique consiste en l’appariement d’un référent donné à tous ses dessins, elle est alors définie comme l’ensemble des couples formés de deux termes, le premier terme étant le référent, le deuxième terme étant pris dans l’univers de tous les dessins possibles du référent. Le terme figure géométrique renvoie dans cette acceptation à l’établissement d’une relation entre un objet géométrique et ses représentations possibles. Dans cette approche, les rapports entre un dessin et son référent construits par un sujet, lecteur ou producteur du dessin, constituent le signifié de la figure géométrique associé pour ce sujet. Ce signifié correspond à ce que Fishbein (1993) appelle figural concept ”.

Ainsi, du point de vue de la modélisation, il est adéquat de distinguer figure et dessin: la figure est l'objet euclidien pris comme domaine de réalité tandis que le dessin est une matérialisation de la figure sur le papier, le sable ou l’écran de l’ordinateur, un modèle (Laborde, 1994). Ce dernier présente des règles et des conventions implicites: le tracé est toujours imprécis et les informations licites que l'on peut tirer du dessin ne sont pas déterminées par le seul dessin mais par un discours accompagnant le dessin (Duval, 1988).

(Laborde, 1994 p 3)

Cette description nous semble la plus pertinente pour distinguer entre dessin et figure car elle considère le dessin comme un modèle d’un domaine de réalité, le référent théorique, ce qui est souvent le cas dans l’enseignement de la géométrie euclidienne plane, à partir de la classe de 3ème (4ème française). C’est cette définition du dessin que nous adopterons dans ce travail de recherche.

Les difficultés des élèves liées à l'interprétation des dessins, en tant que modèles de figures, concernent la résistance à éliminer les imperfections du tracé que le mathématicien élimine de façon machinale pour ne travailler que sur un dessin infiniment précis (Arsac, 1989 a). Au delà des bruits dus à l’imprécision du tracé, la figure présente plusieurs aspects dont quelques uns seulement apparaissent pertinents pour la résolution du problème et sont, par conséquent, pris en compte et traduits en termes géométriques. Une autre difficulté consiste en la non reconnaissance de l'invariance de la figure pour des positions différentes du dessin (phénomènes de typicalité, exemples prototypiques…). De plus, l'attraction de certains aspects du dessin entrave une analyse géométrique. Ainsi le passage du dessin à la figure ne va pas de soi car l'élève reste à une vue très empiriste de la géométrie.

Relativement au dessin, nous essayerons d’identifier, dans l'élaboration d’une démonstration par l’élève, les éléments des pas de la démonstration qui trouvent leur source non dans les théorèmes et définitions mais dans l'appréhension perceptive du dessin. Ainsi, nous tenterons, à partir de cette étude, d'évaluer le degré de détachement de l'élève du dessin et sa capacité à élaborer une justification des résultats conformément à la théorie de la géométrie euclidienne

III.1.3 Organisation déductive de la démonstration

Dans la situation traditionnelle d’enseignement, une démonstration est d’abord un texte qui répond à certaines normes, allant des hypothèses aux conclusions, énonçant correctement les théorèmes utilisés (Barbin, 1996). Cette description, reflétant comment s’organise une démonstration, correspond bien à la définition de la démonstration donnée par Balacheff (1988), expliquant comment se structure une démonstration et adoptée dans cette recherche « Il s'agit d'une suite d'énoncés organisée suivant des règles déterminées: un énoncé est connu comme étant vrai ou bien est déduit à partir de ceux qui le précèdent à l'aide d'une règle de déduction prise dans un ensemble de règles bien défini... Ce qui caractérise les démonstrations comme genre de discours est leur forme strictement codifiée ». Elle rejoint également la description donnée par Duval et Egret (1989) de la structure d’une organisation déductive des énoncés

« La suite des énoncés est produite par substitution d’un nouvel énoncé à un énoncé antérieurement donné (comme hypothèse ou comme résultat d’une substitution déjà effectuée). Cette substitution s’effectue explicitement en vertu d’un énoncé normatif (une définition, un axiome ou un théorème) qui fonctionne comme règle permettant cette substitution ».

Les descriptions données par Balacheff, Duval et Egret mettent en évidence une unité fonctionnelle dans la démonstration qui est le pas de la démonstration, appelé aussi arc transitif de substitution (ATS), selon les termes de Duval et Egret. Dans ce pas, un énoncé tiers (règle de substitution), pris dans une théorie bien déterminée, explique le passage des hypothèses à la conclusion. Ainsi, la démonstration se structure en une suite de pas (ATS) qui ont tous la même structure et qui correspondent à une démonstration de longueur minimale, ce qui lui donne une « forme strictement codifiée ».

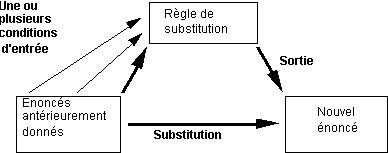
Duval et Egret (1989)

Dans le schéma ci-dessus, emprunté à Duval et Egret (ibid), il apparaît que l’ATS a une structure ternaire et non binaire. En effet, celui-ci comporte trois énoncés ayant chacun un statut différent. En mathématiques, la règle de substitution peut ne pas être écrite afin de ne pas alourdir le texte de la démonstration. Cependant, dans une situation d’apprentissage, nous estimons qu’il est important que l’enseignant marque la place fonctionnelle de cette règle, au moins oralement. En effet, nous considérons que dans une démonstration « les énoncés s’articulent en raison de leur statut et ce statut est indépendant de leur contenu » (Duval et Egret, ibid). D’une situation à une autre, un énoncé peut changer de statut (hypothèse, conclusion) alors qu’il garde le même contenu.

Par ailleurs, dans une situation d’apprentissage, il est possible que l’élève interprète, autrement que par une règle de substitution, le passage d’une hypothèse à une conclusion. En effet, l’élève interprète, souvent, ce passage en s’appuyant sur des données visuelles fournies par le dessin. Ainsi, nous considérons que si la structure de la démonstration comme suite d’ATS, dans laquelle une règle de substitution explique le passage de l’hypothèse à la conclusion, n’est pas perçue par l’élève, cela favoriserait davantage le recours à des démarches de type empirique. De ce fait, il nous a semblé intéressant d’étudier si l’élève est conscient de cette structure de la démonstration, et de voir dans ce cas quels sont les théorèmes explicités et ceux qui ne le sont pas.

 La question de décider de la nécessité d’expliciter, dans une démonstration, certains théorèmes et non d’autres peut se poser aussi chez les enseignants et dans les manuels. Nous nous proposons de rechercher une réponse à cette dernière question, en étudiant, dans un pas de démonstration, si l’énoncé tiers est explicité ou ne l’est pas. Le contrat didactique joue un rôle dans la détermination du niveau d’explicitation, qu’il s’agisse du contrat dans les manuels ou celui en classe de mathématiques. Nous envisageons d’étudier, dans les manuels et auprès des enseignants et des élèves, si les règles de substitution sont explicitées ou non, ceci dans diverses classes de 4ème (3ème française) ayant, a priori, des niveaux différents et appartenant à plusieurs établissements scolaires. Cela constituera, dans cette recherche, l’étude du pôle “ Explicitation de la règle de substitution ” dans une démonstration.

III.1.4 L’heuristique

Dans la littérature, ce terme renvoie à ce qui sert à la découverte ou ce qui consiste à faire découvrir ce que l’on veut enseigner (Robert, 1993). En intelligence artificielle, il évoque une méthode de recherche fondée sur l'approche progressive d'un problème. En psychologie, l’heuristique est une règle d'action applicable à toute situation, qui permet la plupart du temps d'aboutir plus rapidement à la solution. Elle se distingue de l'algorithme qui est une règle qui permet d'arriver à la solution, dans tous les cas[2].

De nombreux travaux de recherche, consacrés à la résolution des problèmes ou à la démonstration, se sont intéressés à l’heuristique. Polya (1967) appelle heuristique “ l’étude des procédures et des méthodes de résolution des problèmes ”. Cette définition est reprise et explicitée par Polya (1980): « L’heuristique est l’étude des chemins et moyens de découverte et d’invention; elle étudie spécialement, dans la résolution des problèmes, ces étapes qui se présentent souvent et naturellement et qui ont quelque chance de nous rapprocher de la solution ».

Pour Pluvinage (1977), il existe des questions qui font peu ou pas appel à l’heuristique, qu’il appelle automatismes. A l’opposé, d’autres questions dans lesquelles les méthodes de résolution ainsi que les notions mathématiques à faire intervenir sont des objets des recherche ont des solutions qui relèvent du domaine de l’heuristique.

Pour Glaeser (1976), l'analyse peut être synonyme d'heuristique dans le sens qu'elle est liée à l'invention imaginative qui exige intuition, talent et fantaisie. Elle évoque aussi le calcul qui devrait mener sûrement à la solution (Algorithme). A l’analyse, il oppose la synthèse qui peut être synonyme de dissimulation de l'heuristique “ lorsque la recherche a été menée à bien, il reste à gommer toute allusion à la démarche qui a servi à trouver la solution et d'éliminer tous les pas inutiles pour aboutir à un discours aussi concis que possible ”.

Les descriptions données ci-dessus par Polya, Pluvinage et Glaeser, définissant l’heuristique, renvoient toutes à la phase de recherche permettant d’aboutir à la solution d’un problème et liée, selon certains, à l’invention ou à l’intuition. Cette phase de recherche retrouve toute son importance dans l’enseignement heuristique apparu, il y a une vingtaine d’années, aux Etats Unis et au Canada (Paquette, 1980 a). L’enseignant intervient par des questions incitant l’élève à utiliser des éléments de méthode pour la résolution des problèmes (des heuristiques). Cet enseignement vise de créer une atmosphère de recherche qui fait revivre à l’apprenant, compte tenu de son niveau de connaissance et de développement intellectuel, un peu de l’activité du mathématicien (Paquette, 1980 b).

Dans ce travail, nous projetons d’étudier, dans la démonstration rédigée par l’élève, des indices qui peuvent renseigner sur cette phase de recherche et si elle a été faite adéquatement. Cette étude ne pourra pas renseigner sur tout le travail de recherche de l’élève mais sur quelques uns de ses aspects, repérés à partir de ses traces sur la copie. En effet, comme le précise Barbin (1996), « Une démonstration indique le bon chemin, bien différent du cheminement de la recherche. Car la mise en forme déductive efface toute trace des questionnements, des zones d’instabilité, des tensions qui sont le prélude au désir et au besoin de démontrer ». Toutefois, comme l'a précisé Arsac (1996), "On peut penser que toutes les évidences qui figurent dans le raisonnement final sont intervenues dans la recherche et même que ce sont les plus solides parmi celles qui ont été envisagées".

Dans la démonstration fournie par l'élève, il n'est pas possible d'étudier les différentes tentatives de résolution qui ont abouti à la solution fournie (Plan régressif ou travail en arrière selon Polya (op. cit); travail d'analyse, selon l'appellation des géomètres grecs). La solution sera étudiée à partir d’une démonstration rédigée par l'élève sur la copie (La tâche complémentaire d'exécution appelée progressive ou travail en avant selon Polya (ibid); travail de synthèse, selon l'appellation des géomètres grecs) et pourra nous fournir des indices sur la recherche qu’il a faite. Par exemple, il sera possible d’étudier si un élève connaît les théorèmes de cours et les mobilise adéquatement dans une démonstration. L’utilisation d’une conclusion comme hypothèse du problème sera un indice renseignant sur une recherche inadéquate de la solution.

Ces choix nous amènent à ne pas adopter les appellations “ Heuristique ” et “ Recherche de la solution ” car elles ne traduisent pas fidèlement ce que nous recherchons. Nous désignerons ce pôle d’étude par “ Structure de l’enchaînement de la solution ”. Cette phrase renverra, dans la démonstration rédigée par l’élève, à la structure de la procédure de l’élève, de la ligne d'action qu'il a suivie, le schéma des opérations qui lui ont paru logiques, pour lui permettre, en partant de l'hypothèse du problème, d'aboutir à la conclusion. Cette caractérisation rappelle ce que Polya (ibid) définit comme solution d’un problème de démonstration « Une suite d’opérations logiques articulées, une suite d’étapes, qui part de l’hypothèse et finit à la conclusion désirée du théorème ». Dans l’étude de ce pôle, nous exclurons celle des démarches des élèves relatives au dessin. Ce dernier, sur lequel s’appuie, sans doute, la phase heuristique, est étudié à part et constitue l’un des pôles de notre recherche.

Dans le schéma ci-dessous, nous résumons les différentes recherches sur la démonstration que nous avons déjà présentées (II. Problématique de la démonstration) et nous introduisons notre recherche centrée sur les quatre pôles que nous venons d’expliciter (La formulation mathématique, le dessin, l'explicitation de la règle de substitution et la structure de l'enchaînement de la solution).

III.2 Problématique de la recherche

Nous avons explicité les différentes raisons qui nous ont poussé à choisir la démonstration comme objet d’étude. L’une des raisons les plus motivantes était le constat de l’échec d’élèves, que ce soit sur le plan des résultats ou sur le plan de l’assimilation de la notion même (Arsac 1988), et la difficulté des enseignants à apprendre à leurs élèves, qu’ils considèrent “ non doués ”, à faire correctement des démonstrations. Nous nous sommes alors posées un ensemble de questions et d’hypothèses concernant les enseignants et les élèves tunisiens que nous allons énumérer dans ce paragraphe. Une première question générale concernant les enseignants est la suivante:

Q1P: Comment les enseignants tunisiens envisagent l’enseignement de la démonstration?

Les manuels et les programmes tunisiens insistent sur la forme de la démonstration et non sur son sens, et nous considérons qu’il est peu probable que les enseignants qui suivent le programme et sont contraints de le terminer dans les délais fixés pensent à faire le contraire. Ainsi, nous adoptons comme hypothèse de travail, ce qui suit:

H1P: Les enseignants tunisiens orientent l’enseignement de la démonstration sur sa forme, comme il est le cas dans les manuels et les programmes.

Cette première hypothèse nous conduit à nous interroger sur leurs exigences de forme à propos de l’élaboration d’une démonstration par un élève de 4ème (3ème française), niveau scolaire sur lequel s’est fait notre choix. Nous avons trouvé intéressant d’essayer d’identifier ces exigences à partir de l’évaluation qu’ils font de copies d’élèves. Cette méthode de travail, qui n’a pas été utilisée jusque là dans les recherches sur le problème d’enseignement et d’apprentissage de la démonstration, présente l’avantage de permettre de mieux cerner les exigences des enseignants par rapport à une démonstration écrite que celle de l’observation d’une séance de classe. En effet, nous estimons qu’il y a moins de variables qui interviennent lorsqu’il s’agit d’un enseignant face à une copie d’élève qu’un enseignant face à un groupe d’élèves, en présence d’un observateur extérieur. Ainsi, nous nous posons cette question plus précise:

Q2P: Quelles sont les exigences des enseignants de 4ème (équivalent 3ème française) dans la rédaction d’une démonstration par un élève de 4ème?

Nous considérons que les exigences des enseignants peuvent concerner de nombreux aspects dans la rédaction d’une démonstration, qu’il est difficile de prendre en compte, de façon exhaustive. Pour mener à bien notre étude, et en nous inspirant de différentes étapes d’élaboration d’une démonstration en géométrie, dans une situation habituelle de classe de mathématique, et de nombreux travaux de recherche sur la démonstration, nous décidons de restreindre les caractéristiques étudiées et de n’en retenir que quatre. Il s’agit des quatre pôles que nous avons présentés dans la partie théorique et que nous pouvons repérer dans une démonstration rédigée par l’élève: le dessin, la formulation mathématique, l’explicitation de la règle de substitution et la structure de l’enchaînement de la solution.

Cependant, si nous admettons que les exigences des enseignants à propos de la démonstration concernent ces quatre pôles, il nous semble intéressant d’essayer d’identifier, parmi ces derniers ceux qui sont plus importants que d’autres. Ainsi, nous nous sommes posées la question suivante à laquelle nous nous proposons de répondre au cours de ce travail de recherche:

Q3P: Quel est le degré d’exigence relatif à chaque pôle, des enseignants tunisiens?

Les réponses qu’envisage d’apporter ce travail de recherche à ces questions permettra de repérer certains effets du contrat autour de la démonstration. D’autre part, il nous a semblé important, pour compléter l’étude du contrat didactique s’établissant autour de la démonstration, de centrer une partie de la recherche sur l’étude des démarches de rédaction d’élèves de 4ème tunisienne (3ème française), relatives à un problème de démonstration en géométrie. Une première question générale s’est imposée:

Q1E: Quelles sont les difficultés que rencontrent les élèves dans la rédaction d’une démonstration?

En nous appuyant sur les travaux de Duval et Egret (1989), nous admettons l’hypothèse de travail suivante:

H1E: Les difficultés des élèves, dans la rédaction d’une démonstration, sont liées à un manque de connaissance de la structure ternaire d’un pas de la démonstration et de la nature de l’élément explicatif dans ce pas.

En tenant compte de cette hypothèse, nous nous sommes proposées d’étudier le type d’explication donné par un élève au passage d’une hypothèse à une conclusion, dans un pas de la démonstration. Pour cela, nous avons crée un nouveau type d’activité, basé sur la réalisation d’un QCM et nous nous sommes posées la question suivante:

Q2E: Outre le dessin et les énoncés de cours, quelles sont les sources dans lesquelles l’élève trouve une explication au passage d’une hypothèse à une conclusion, dans un pas de démonstration?

Enfin, nous espérons que l’expérience que nous envisageons de mener auprès des enseignants et des élèves permettra d’apporter des éléments de réponses à la question suivante, concernant ces deux pôles du système didactique:

QPE: Est-il possible de déceler des corrélations entre les exigences des enseignants et les types de procédures d’élèves, dans l’élaboration d’une démonstration?

Nous signalons que des hypothèses plus fines concernant les enseignants et les élèves seront émises dans les paragraphes “ Analyse a priori ” relatifs aux chapitres C et D de la thèse.