Activité 2 p 37-38

--------------------------------------------------------------------------------------

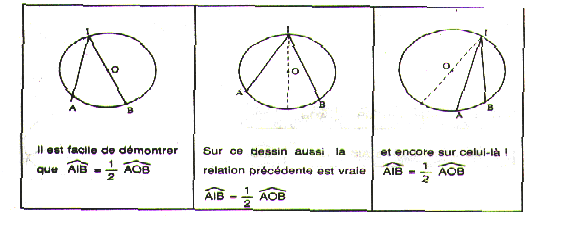
a) Un de tes camarades a trouvé dans un vieux livre de mathématiques les dessins et les commentaires suivants.

b) On te donne ci-après la démonstration du premier cas.

Démonstration

 Le triagle IOA est isocèle de sommet principal O.

AOB est l'angle extérieur en O au triangle IOA d'où

AOB       = OIA + OAI

                = 2 AIB car le triangle IOA est isocèle

AOB       = 2 AIB s'écrit aussi AIB = 1/2 AOB

c) Démontre les deux autres cas, en t'inspirant de ce qui précède

d) Observe la figure ci-contre et complète ce qui manque

ABI = 1/2 ......

IAB = 1/2 ......

AIB =180°-(IAB +.....)

d'où AIB = 180°- 1/2 AOB

----------------------------------------------------------------------------

Dans cette activité, l'énoncé du problème n'est pas donné. Trois dessins sont fournis, représentant chacun un cas particulier d’une même situation (L’angle inscrit dans un cercle est égal à la moitié de l’angle au centre). Chaque dessin, représentant trois points du cercle (A, I et B) et le centre O, est accompagné de la relation à démontrer (AIB=1/2AOB). Le premier dessin correspond au cas B (ou A) est un point de la droite (OI), le second représente les points A et B de part et d’autre de (OI), et dans le dernier, A et B sont du même côté que (OI). Le codage utilisé par le manuel pour différencier ces trois cas est la représentation de la droite (OI) en pointillés dans les cas 2 et 3.

Nous considérons que l’absence de commentaires explicatifs peut poser un problème à l’élève. En effet, si certains codages sont donnés, ils n’expliquent pas à l’élève la raison de donner trois dessins différents pour démontrer la même relation et ne lui permettent pas de savoir qu’une démonstration différente est exigée pour chaque cas.

De plus, nous estimons que même en présence des codages du dessin, une difficulté se présente à l'élève: en l’absence de l’énoncé du problème, il est difficile à ce dernier de déterminer les hypothèses du problème afin de les utiliser dans la démonstration demandée. Le risque d'une telle démarche est que, dans d'autres problèmes posés à l'élève, ce dernier apprenne à considérer certaines constatations sur le dessin comme données du problème, ce qui peut engendrer une confusion dans le statut des énoncés. De plus, plusieurs éléments manquent à la figure et doivent être rajoutés par l’élève pour qu’il puisse faire démonstration.

Par ailleurs, la démonstration donnée dans le premier cas est complète. Le travail de l'élève consiste à faire la démonstration dans les deux autres cas. Dans la démonstration donnée par le manuel, le statut des énoncés n'est pas spécifié par les expressions “ hypothèse ” et “ conclusion ”. Quelques connecteurs sont utilisés (d’où, car), mais non dans tous les pas de démonstration. De plus, certaines conclusions sont données sans que les hypothèses qui les justifient ne soient précisées (Par exemple, dire que IOA est isocèle de sommet principal O sans préciser que I et A appartiennent au cercle de centre O). Il y a un risque de pousser les élèves à établir des relations entre les objets géométriques, à partir de constatations sur le dessin (puisque celui-ci les justifient) et non à partir des hypothèses du problème.

Quant aux règles de substitution, aucune n'a été explicitée. Dans la question b, la démonstration nécessite la mobilisation des propriétés "Dans un triangle, l'angle extérieur est égal à la somme des deux angles intérieurs non adjacents" et "Dans un triangle isocèle, les deux angles à la base sont égaux". Dans la question d, la démonstration utilise les propriétés "L'angle inscrit est égal à la moitié de l'angle au centre" et "Dans un triangle, la somme des angles d'un triangle est égale à 180°). Ces propriétés ont été enseignées à différents niveaux scolaires précédents et aucune d'entre elles n'a été explicitée.

Comme nous l’avons précisé ci-dessus, un dessin a été fourni, dans chacun des cas illustrant l’égalité AIB=1/2AOB. Le premier aiderait l’élève à mieux comprendre la démonstration donnée dans l’ouvrage et correspondant au premier cas. Les deux autres serviraient à l’élève de support afin qu’il puisse structurer la démonstration, dans les deux autres cas. Un quatrième dessin, illustrant un angle obtus inscrit dans un cercle, est donné, en fin d’activité, et il est demandé à l’élève, en “ observant la figure ci-contre ” de compléter une démonstration aboutissant à l’égalité “ AIB=180°-1/2 AOB ”.

Ainsi, dans la démonstration fournie par l’ouvrage et dans les trois autres qui sont censées être faites par les élèves, le dessin a été fait par les auteurs du manuel, ce qui ne fait que renforcer l’idée de l’intérêt que lui accordent ces derniers, dans une démonstration.