N. d'ordre: 1302

RESUME pag.1
INTRODUZIONE pag.3

PREMIERE PARTIE
Chapitre 1 Introduction pag.7
Capitolo 1 L'ostacolo epistemologico : Una prima sistemazione
Introduzione pag.9
1.1.0 Enriques e gli "errori" in Matematica pag.9
1.1.2 Gli "Errori" e la comunicazione delle matematiche pag.10
1.2.0 La Nozione di ostacolo epistemologico: Bachelard pag.12
1.3.0 Gli ostacoli epistemologici nella comunicazione delle matematiche pag.13
1.3.1 Ostacoli di origine ontogeneica pag.13
1.3.2 Ostacoli di origine didattica pag.14
1.3.3 Ostacoli epistemologici nelle matematiche pag.14
1.3.4 Cosa e' una concezione pag.15
1.3.5 Carattere dialettico del processo del superamento di un Ostacolo pag.17
1.4.0 Relazione ostacoli-storia pag.18
1.5.0 Conclusione pag.19
Bibliogafia pag.21
Chapitre 1 Conclusion pag.23

Chapitre 2 Introduction pag.25
Capitolo 2 Esempi di Ostacoli e Teoria delle situazioni
2.1 Cenni alla teoria delle situazioni pag.27
2.2 Gli ostacoli epistemologici nella ricerca francese pag.31
2.2.1 Un primo esempio di ostacoli epistemologici: Gli Interi pag.31
2.2.2 a)Un secondo esempio di ostacolo epistemologico: il limite - Il lavoro di B.Cornu pag.33
b)Il lavoro di A. Sierpinska pag.34
2.2.3 Un terzo Ostacolo epistemologico: Il Valore assoluto (Difficolta' maggiori per una nozione minore) Duroux. pag.37
2.3 Osservazioni conclusive pag.38
Appendice 1 La modellizazione della nozione di situazione attraverso quella di gioco pag.40
Appendice 2 Indice della tesi di B.Cornu. pag.41
Bibliografia pag.42
Chapitre 2 Conclusion pag.43
 

DEUXIEME PARTIE pag.45
Chapitre 3 Introduction pag.47
Capitolo 3 Alcune osservazioni sul linguaggio
3.1.1 Introduzione pag.49
3.1.2 Linguaggio sintattico pag.51
3.1.3 Le limitazioni di un sistema formale: I due teoremi di Gîdel pag.53
3.1.4 I modelli sintattici pag.55
3.2 I Modelli semantici pag.56
3.3 Modelli astratti pag.59
3.4 La riflessione oggi sui fondamenti: Risvolti su dicsipline recenti come Informatica, Cibernetica, Intelligenza Artificiale pag.60
3.5 Il Problema del significato (La semantica) pag.62
3.6 La Pragmatica e i Paradossi pag.64
3.7 Conclusioni pag.69
Bibliografia pag.70
Chapitre 3 Conclusion pag.72

Chapitre 4 Introduction pag.73
Capitolo 4 Le matematiche come linguaggi pag.75
4.1 Introduzione pag.76
4.2 La storia interna delle Matematiche pag.79
4.3.1 La comunicazione delle matematiche (Didattica delle Matematiche)pag.80
4.3.2 Le matematiche nella realta' pag.80
4.3.3 Definizione di Ostacolo epistemologico pag.81
4.3.4 Paradossi e ostacolo epistemologico pag.82
Bibliografia pag.84
Chapitre 4 Concluson pag.85

Chapitre 5 Introduction pag.87
Capitolo 5 Una classificazione degli Ostacoli ed il loro possibile superamento
5.0 Le ipotesi ammesse dalla Neurofisiologia pag.89
5.1 I conflitti (Cognitivo, Socio-Cognitivo, Affettivo) pag.90
5.2 Ostacolo genetico pag.93
5.3 Ostacolo Ontogenetico pag.93
5.4 Ostacoli epigenetici pag.94
5.4.1 Ostacoli epistemologici pag.95
5.4.2 Ostacoli Didattici pag.96
5.5 Conclusioni pag.97
Bibliografia pag.99
Chapitre 5 Conclusion pag.101
 

TROISIEME PARTIE pag.103
Chapitre 6 Introduction à la vérification expérimentale
Chapitre (Complet) pag.105
Capitolo 6 L'ostacolo epistemologico e il Postulato di Eudosso-Archimede
6.0 Introduzione alla verifica sperimentale pag.109

Chapitre 7 Introduction pag.115
Capitolo 7 Postulato di Eudosso-Archimede: Considerazioni storiche ed epistemologiche pag.115
7.1.0 Introduzione pag.115
7.1.1 Perche' il Postulato di Eudosso-Archimede pag.116
7.1.2 Grandezze omogenee e archimedeicita' pag.117
7.1.3 Le concezioni del Postulato di Eudosso-Archimede nella storia pag.118
7.1.4 Il Postulato e L'Infinito (Attuale e Potenziale) pag.119
7.2.0 Il ruolo del P.A. nei fondamenti delle matematiche: Geometria Elementare, Aritmetica, Analisi pag.120
7.2.1 Geometria Elementare pag.121
7.2.3 Aritmetica pag.123
7.2.4 Analisi Classica pag.123
7.3 Tabella riassuntiva sulle concezioni matematiche dell'infinito/infinitesimo attuale e potenziale pag.126
7.4 Conclusione (Schema di riferimento storico) pag.127
TABELLA 1 pag.128
Bibliografia pag.129
Chapitre 7 Conclusion pag.131

Chapitre 8 L'histoire de la recherche (résume) pag.133
Capitolo 8 La storia del lavoro sperimentale
8.1 Introduzione : Il Primo lavoro sperimentale pag.135
8.2 L'esperienza sull'Esaustione pag.136
8.3 Una situazione sperimentale con l'uso del computer (Programma messo a punto con il linguaggio LOGO) pag.137
8.4 Un questionario sulle concezioni spontanee del P.A. a degli insegnanti di Scuola Elementare pag.143
8.5 Lo stato della ricerca oggi pag.144

Chapitre 9 Analyse a-priori du questionnaire de la derniére experience. (résume) pag.145
Capitolo 9 L'analisi apriori del questionario
9.1 Analisi apriori delle conoscenze spontanee sul Postulato di Eudosso-Archimede pag.147
9.2 Analisi apriori del Modello del "Veronese" pag.156
9.3 Analisi apriori del questionario della X,1 pag.158

Chapitre 10 Analyse des donnes expérimentales. (résume) pag.167
Capitolo 10 Analisi dei dati sperimentali
10.1 La scelta del campione pag.169
10.2 Analisi dei questionari pag.171
10.3 Giustificazioni ai quesiti del questionario pag.178

Chapitre 11 Conclusions pag.183
11.1 Considérations sur l'approche sémiotique des mathématiques pag.184
11.2 Nouvelle définition et classification des obstacles épistémologiques pag.184
11.3 Confrontation avec la nouvelle définition: introduction aux hypothéses pag.184
11.4 Définition opérationnelle d'Obstacle épistémologique pag.185
11.5 Hypothéses pag.186
11.6 Démontrer que le Postulat d'Eudoxe-Archiméde est un Obstacle épistémologique pag.187
11.7 Les manifestations prévues suivant les hypothéses pag.187
11.8 Résume des questions et des variables de comportement pag.188
11.9 Les variables de la situation pag.189
11.10 Le plan d'expérience. Matrice explicative. Méthode. pag.189
11.11 Analyses et Résultats pag.190
11.11.1 Analyse des fréquences de réussite pag.190
11.11.2 Analyse des données pag.191
11.11.3 Analyse implicative pag.192
11.12. Conclusions et perspectives pag.193

PA1 F.Spagnolo-C.Margolinas, Un Ostacolo Epistemologico rilevante per il concetto di limite: Il Postulato di Archimede, La Matematica e la sua Didattica, Ed. Il Pitagora, Bologna, n.4, 1993. pag.196

PA1F Une version francais du PA1. pag.215

PA2 F.Spagnolo-S.Camarda, Angoli di contingenza e Analisi non Standard, La Matematica e la sua Didattica, Roma, Ed.Armando Armando, n.3, 1989. pag.225

PA2F F.Spagnolo-S.Camarda, Angles de contingence et Hiperreels, Une version francais du PA2. pag.232

PA3 F.Spagnolo-T.Marino-M.V.Di Leonardo, Alcune osservazioni didattiche ed epistemologiche sul Postulato di Eudosso-Archimede ed il metodo di Esaustione, La Matematica e la sua didattica,
Bologna, n.1, 1994. pag.239

PA4 Programma in linguaggio LOGO di una esperienza didattica. pag.252

PA5 Griglia di analisi dell'esperienza relativa a PA4. pag.258

PA6 Questionario sul Postulato di Archimede somministrato ad Insegnanti di Scuola Elementare. pag.259

STAT-0 Analisi dei dati relativi ai questionari somministrati nel Nov.1994. Distribuzione di frequenza, voto di diploma e provenienza scolastica dalle scuole secondarie superiori. pag.260

STAT-PA6 Analisi statistica dei dati relativi al questionario PA6. pag.262
Analyse en Composantes Principales

STAT-1 Medie e scarti relativi alle variabili. pag.268

STAT-2 Correlazione gerachica di Spermann. pag.269

PA7 Pietro Tortorici, Quaderni Didattici sulle Matematiche Complementari, Quaderno n.11, Ed. Arti Grafiche A.Renna, Palermo, 1952, pagg.59-71, Sui Continui non Archimedei. pag.271

QUEST-VERONESE 1^ Version (Ottobre 1994) pag.279

QUEST-0- 2^ Version (Ottobre 1994) pag.281

QUEST-0-1^ Version (Settembre 1994) pag.284

QUEST-X,1- 1^ Version (Settembre 1994) pag.287

QUEST-X,1- 2^ Version (Ottobre 1994) pag.299

QUEST-0-F Questionario riguardante le concezioni spontanee sul Postulato di Eudosso-Archimede.(Novembre 1994) pag.307

QUEST-VER.-F Questionario sul Modello del Veronese. (Novembre 1994) pag.311

QUEST-X,1-F Questionario sulla X,1. (Novembre 1994) pag.312

QUESTIONNAIRE NON EXPERIMENTE : Aprossimation à Q. pag.317

QUESTIONNAIRE NON EXPERIMENTE : Modele droite reelle. pag.321

QUESTIONNAIRE NON EXPERIMENTE : Infini/Infiniment petit. pag.322

STAT-3 Analyse en Composantes Principales pag.324 (107 éléves - 24 variables)

STAT-4 Analyse Factorielle des correspondances simples (107 éléves - 24 Variables actives - 5 variables supplementaires) pag.329

STAT-5 Analyse Factorielle des Correspondances simples (107 éléves - 24 Variables actives - 5 variables supplementaires - 2 observations correspondant au profil Obstacle (So1) et non-Obstacle (So2) pag.332

Chapitre 10 Analyse des donnes expérimentales (version francaise) pag.348

Questionnaires annexes (version fran*aise) pag.356

Liste des variables complets pag.363

Liste des variables sur lesquelles on a fait l'analyse des donnes pag.365
 

L'objet de la recherche peut se présenter :

1- Est-il possible de donner une définition d'Obstacle épistémologique opératoire
qui est soutenu par une interprétation sémiotique des Mathématiques?

2- Le Postulat d'Eudoxe-Archiméde est-il un Obstacle épistémologique?

3- Est-il possible de donner des instruments opératoires pour franchir des Obstacles
épistémologiques ?
 
 

Pour chercher de répondre à ces questions on a suivi le parcours:

1- La premiére partie de la thèse (chapitres 1 et 2) présente la notion d'obstacle et sa place dans la recherche en Didactique du point de vue théorique et expérimentale.
Il s'agit d'examiner les différents sens donnes à ce concept (dans diverses théorisations) et de le confronter aux résultats expérimentaux obtenus par diverses mèthodes.

2- La seconde partie (chapitres 3, 4, 5) pr*sente une nouvelle définition de la notion d'obstacle épistémologique en utilisant un nouveau cadre : celui d'une interprétation sémiotique des langages mathématiques et mis au point d'un Modèle théorique-expérimental pour l'individuation des obstacles épistémologiques.
Cette nouvelle définition est utilise pour proposer une classification des obstacles.

3- La troisiéme partie (chapitres 6, 7, 8, 9, 10) montre que le Postulat d'Eudoxe-Archiméde est un obstacle épistémologique au sens introduit dans deuxiéme partie. La démonstration fait appelle à des arguments historique et épistémologique [Chp.7] pis à une étude expérimentale (Modèle).
L'étudie expérimental consiste en l'élaboration d'un ensemble de situations et de comportements spécifiques puis à leur confrontation à un échantillon de 107 éléves de DEUG en Mathématique.
Les résultats statistiques confirment que le Postulat d'Eudoxe-Archiméde est un obstacle épistémologique.

4- La thése est accompagnée [voir les Annexes] des trois articles déjà parus dans des revues italiennes et qu'aident à argumenter la discussion sur les hypothèses.

Les argumentations historiques et épistémologiques sont présentes dans le chapitre 7, mais la plus parte sont présentes dans les Annexes PA1, PA1F, PA2, PA2F, PA3, PA7. La motivation de ce choix (présenter les argumentations historiques et épistémologiques dans les annexes) est due au fait qu'on a voulu montrer le Modèle théorique-expérimental pour la détermination des obstacles épistémologiques et tout ca est indépendant du choix du contenu mathématique objet de recherche.

Le Ipotesi di ricerca della tesi sono connesse alle seguenti domande

1- E' possibile fornire una definizione di Ostacolo Epistemologico che sia operativa e che tenga conto di una lnterpretazione semiotica delle Matematiche ?

2- Il Postulato di Eudosso-Archimede e' un Ostacolo Eplstemologico ?

3- E' possibile fornire degli strumenti operativi per il superamento degli ostacoli epistemologici ?
 

Per cercare di rispondere a queste domande si e' seguito il segucnte percorso:

1- Nella I parte della tesi composta dai capitoli 1 e 2 si é analizzato il signiflicato di ostacolo nella ricerca in didattica sia da un punto di vista teorico che sperimentale. Questo primo momento ha lo scopo di lntrodurre il Modello ostacolo nelle teorizzazioni didattiche mettendolo il relazione con le metodologie sperimentali per individuare gli ostacoli.

2- Nella Il parte composta dai capitoli 3, 4, 5 si cerca di argomentare la prima ipotesi della tesi e cioé quella riguardante la messa a punto di un Modello per l'individuazione di ostacoli attraverso una riorganizzazione semiotica dei Linguaggi Matematici. La II parte si conclude con una definizione di ostacolo epistemologlco ed un tentativo di classificazione degli ostacoli.

3- Nella III parte composta dal capitoli 6, 7, 8, 9, 10 si tenta di dimostrare, attraverso il Modello sull'ostacolo epistemologico definito nella II parte, che il Postulato di Eudosso-Archimede e' un ostacolo eplstemologico. La dimostrazlone si avvale oltre che di una analisi storica ed epistemologica anche di una analisi statistica Le argomentazioni storiche ed epistemologiche sono in parte presentate nel capltolo 7, ma in gran parte presentate negli allegati PA1, PAlF, PAZ, PA2F, PA3, PA7. La motivazione di una tale scelta, quella cioe' di presentare le argomentazioni storiche ed epistemologiche negli allegati, e' dovuta al fatto che si e' voluto mettere in evidenza il Modello teorico-sperimentale per la determinazione degli ostacoli epistemologici e questo risulterebbe indipendente dalla scelta dell'argomento matematico oggetto di indagine.

Il campione utilizzato per l'analisi statistica dell'ultimo questionario presentato nella ricerca e' costituito da 107 allievi del primo anno del Corso dl Laurea in Matematica della Facolta' di Scienze dell'Universita' di Palermo.

4- La tesi é corredata da tre articoli già pubblicati su riviste italiane che aiutano ad argomentare le ipotesi.

Il lavoro é rivolto sostanzialmente ai seguenti soggetti :

1- Agli lnsegnanti per poter meglio comprendere il sapere degll alllevi e riflettere sulla loro epistemologia;

2- Al ricercatore in Didattica delle Matematiche per poterlo utilizzare come strumento per la formazione degli insegnanti uno del possibili percorsi per poter ripensare agli ostacoll e/o al Postulato dl Eudosso-Archlmede) e per poter individuare e stimolare riflessioni sull'epistemologia dell'insegnante (e di conseguenza su quella dell'allievo).

Dans la rédaction de la thèse nous nous somme pose plusieurs questions. A quelque question nous avons répondu, à d'autre no.
En particulier nous avons aborde les suivants questions:
1. Les obstacles épistémologiques s'utilisent dans l'enseignement des mathématiques et dans la recherche en didactique des mathématiques. (Chapitre 1)
2. Le passage entre Protomathématique et Mathématique n'explique pas comment on devrait rattraper les sens et les relations entre langages mathématiques dans la communication en didactique des mathématiques. (Chapitre 2)
3. Les mathématiques ont été considére comme des langages avec la suivant classification sémiotique:
a) Un aspect syntactique des mathématiques: Système formel, Modèle syntactiques, Modèle sémantique (Bourbaki);
b) Un aspect sémantique des mathématiques, Théorie du sens, Théorie de la référence (Quine);
c) Un aspect pragmatique des mathématique: Communication, Paradoxes.

Dans cette perspective le langage mathématique nait avec une certaine ambiguté sémantique et est en constante évolution, avec une grammaire qui se réorganise moyennement des réajustements continus. Quand un langage se formalise (comme il en va de certaines théories mathématiques), on assigne un certain sens aux formules et on perd le sens précédent.

De la Pragmatique on utilise les paradoxes. Les paradoxes se divisent en:
a) Paradoxes logico-mathématiques: antinomies (RUSSEL);
b) Paradoxes sémantiques: antinomies sémantiques (RICHARD);
c) Paradoxes pragmatiques: injonctions paradoxales (ou conflit cognitif).

Ce point de vue permet de argumenter de maniére intéressante la recherche des obstacles épistémologiques. En effet on prend la position qu'il faut chercher les obstacles épistémologiques dans la syntaxe des langages mathématiques qu'on veut étudier.
Un exemple éclatant est lie aux Paradoxes de Zénon (400 a.c.) sur l'infini et l'infiniment petit actuel et potentiel. Dans la seconde moitié du XIXe siécle les mathématiciens ont réorganise la grammaire de l'infini/infiniment petit potentiel et avec G.CANTOR la grammaire de l'infini/infiniment petit actuel. Et enfin avec les axiomes de Zermelo-Frankel l'infini est devenu un axiome dans la théorie formelle des ensemble. (Chapitre 7)
On peut considérer les paradoxes logico-mathématiques et sémantiques comme des obstacles épistémologiques puisque dans l'histoire des langages mathématiques ils se sont toujours places autour de la syntaxe des nouveau langage. Par exemple RUSSEL construit la théorie des types pour éviter les Paradoxes logiques.
Un obstacle épistémologique peut se trouver en regardant quand, avec des instruments historico-épistémologiques, on a franchi le Paradoxe à lui lie (c'est le moment de généralisation du langage considére).
Les injonctions paradoxales et les conflits cognitifs, peuvent ils etre considérés comme des indices d'obstacles didactiques puisqu'ils jouent directement un rôle dans la communication? Une bonne partie des problémes ouverts présentés dans les rencontres de Didactique de Mathématique représentent des situations didactiques construites sur des injonctions paradoxales.
Les injonctions paradoxales peuvent-elles caractériser les obstacles épistémologiques?
 
 

11.1. Considérations sur l'approche sémiotique des mathématiques

Quelques considérations sur l'introduction sémiotique des mathématique sont importantes:
1- Une plus évidente corrélation entre la connaissance mathématique (les fondements des langages) et l'évolution historique des mathématiques. L'étude des conceptions historiques n'est pas que l'étude des sens lies à une certain langage dans un détermine pèriode historique;
2- La possibilité de revoir le changement d'un contexte aussi en terme de changement de langage;
3- La possibilité de revoir la généralisation d'un contexte aussi en terme de généralisation de langage.
Ce point de vue permet de donner des informations supplémentaires à la théorie des situations. Le langage, au niveau sémiotique, est considéré un systéme déterminé par des représentations, des opérations et des structures de controle et avec un domaine de validité.

11.2. Nouvelle définition et classification des obstacles épistémologiques

Maintenant on peut donner une nouvelle définition d'obstacle épistémologique, dans une perspective linguistique, que permettra de revoir le modèle de Duroux-Brousseau pour l'individuation des obstacles épistémologiques:
Quand dans une certaine èpoque historique, la communauté mathématique cherche à passer d'un champ sémantique significatif à un nouveau langage relatif à une certaine classe des problémes, entrent en jeu des "objets" mathématiques particuliers.
Définition: Les objets mathématiques des champs sémantiques précédent qui pourraient servir pour la construction syntaxique (dans les fundamenta du nouveau langage) sont les obstacles épistémologiques.
C'est donc dans l'évolution des champs sémantiques du langage mathématiques qui se situent les obstacles épistémologiques: " Des obstacles épistémologiques sont définis en tant qu'objets mathématiques des champs sémantiques précédents qui peuvent etre utilises dans la construction syntactique du nouveau langage. Ce nouveau langage est alors spécifié par rapport à une certaine classe de problèmes (supposés inabordables dans le langage antérieur)."

Le tableau ci dessous prèsente une nouvelle classification des obstacles.
- Obstacle génétique
- Obstacle ontogénétique -------->

- Obstacle epigénétique: a) Obstacle didactique -------> Injonction Paradoxale

b) Obstacle épistémologique ------> Paradoxe Logico-Math.; Paradoxe sémantique

11.3. Confrontation avec la nouvelle dèfinition: introduction aux hypothèses

Les différences avec la définition de DUROUX-BROUSSEAU résident dans le fait qu'il faut adjoindre:
1- Les obstacles mathématiques, en tant qu'objets mathématiques, peuvent se trouver dans la syntaxe des langages mathématiques.
et qu'il faut lire le modèle de facon différente:
2- Au lieu de dire que "aprés la prise de conscience de l'inexactitude de la connaissance-conception, celle-ci continue de se manifester de facon intempestive et persistante", on dira que "aprés la prise de conscience du role de la connaissance-obstacle dans le nouveau langage, les conceptions relatives au role de la connaissance-obstacle persistent dans le langage de départ."
3- Il faut considérer le changement de point de vue qui se produit avec le changement de langage et dans la généralisation du langage, dans la perspective sémiotique.
La reformulation de la définition dans le cadre d'un modéle épistémologique plus général des mathématiques rend plus opératoire la notion d'obstacle épistémologique.
Cette réponse n'est pas bien compréhensible si on ne peut pas la traduire en termes opérationnels, c'est à dire dans un possible Modèle d'Obstacle épistémologique:

Prenons maintenant les deux thèse principales:

T1: Le Postulat d'Eudoxe-Archimede est une connaissance qui peut constituer une obstacle épistémologiquààla compréhension de l'analyse non standard.

T2: Les formes langagiéres des mathématiques interviennent dans la définition des obstacles.

11.4. Définition opérationnelle d'Obstacle épistémologique.

Donner une définition opérationnelle d'Obstacle en général et épistémologique en particuliér fondée sur une enquéte épistémologique des langages mathématiques suivant un point de vue sémiotique. Une telle définition devrait conduire à un Modéle d'Obstacle épistémologique.

1- Les obstacles sont à chercher entre les éléments constitutifs des langages mathématiques qu'on veut étudier. L'analyse se rétrécit sur ce que les mathématiciens appellent fundamenta du langage (Voir 3.6 et chapitre 4).

2- Une fois rétréci le champ d'action, on peut reprendre la classification de Duroux (Chapitre 1) [Revue avec le point 1] pour déterminer si un objet mathématique est un obstacle épistémologique ou non:

a) Un obstacle épistémologique est une connaissance: on peut le vérifier avec des instruments historico-épistémologiques.

b) Cette connaissance produit des réponses adaptées dans un certain contexte fréquemment rencontre: vérification expérimentale à travers des enquetes qui font voir comment s'accumulent les conceptions autour des questions posées dans un contexte détermine avec un langage détermine.
c) Cette connaissance produit des réponses fausses au dehors du contexte. Elle ne réussit pas à transférer des réponses relatives à un contexte divers, soit parce qu'on a changé le point de vue [c1], soit parce qu'on a considéré un contexte plus général [c2] dans lequel la premiére était un cas particulier. On peut le vérifier expérimentalement à travers le changement du contexte en ce qui concerne [c1]. Ces deux moments, c'est à dire le point de vue et la généralisation représentent deux instruments importants pour la construction des langages, soit dans l'histoire des Mathématiques (Voit Chp. 7), soit dans la réorganisation des fundamenta des Mathématiques (Voit Chp. 3 et 4). Donc, étant deux moments importants pour la mise au point des connaissances mathématiques, ils constituent deux moments significatifs pour la caractérisation des obstacles épistémologiques. On peut vérifier expérimentalement à travers un agrandissement du contexte o* on ne peut plus reconnaître le role de la connaissance objet d'obstacle pour ce que regarde [c2]. Cela correspond à un élargissement du langage ou la connaissance, objet d'obstacle, n'est plus reconnue comme élément fondamental (par exemple axiome), mais devrait etre reconnue comme une quelconque propriété du langage.

d) Cette connaissance résiste aux contradictions auxquelles elle est confrontée. Au fond cet aspect, lié au point précédent, consiste plutot en un fait de procédure que d'analyse sur le fundamenta au sens ou la connaissance se présente de la meme maniére quand on reproduit plusieurs fois la meme situation. Les contradictions pourraient naitre des informations supplémentaires, situations didactiques construites ad hoc dans lesquelles devraient etre mis bien en évidence le nouveau role de la connaissance/obstacle, du nouveau langage étendu.

e) Cette connaissance continue à se manifester aussi aprés sa prise de conscience. C'est à dire que aprés avoir prise conscience du role de la connaissance/obstacle dans le nouveau langage, demeurent les conceptions relatives au role de la connaissance/obstacle du langage du départ. Il reste le role du fundamenta du langage de départ. On peut le vérifier expérimentalement dans ce cas encore avec la mise au point de situations didactiques.

Les hypothèses qu'il faut vérifier expérimentalement seront donc les points 1, 2a, 2b, 2c1, 2c2, 2d, 2e qui nous permettent de pouvoir établir si une conception que vérifie le Modèle est un éventuel obstacle épistémologique.

11.5. Hypothèses.

a) Hypothèses soutenues ci dessus avec des argumentations de nature théorique:

H1: Les obstacles épistémologiques sont caracterisables par des modifications "assez profondes" du langage et par des changements de systémes axiomatiques, les fondements des éléments constitutifs des théories et des langages mathématiques.

La preuve pourrait en etre donne par l'examen exhaustif des obstacles actuellement repéres ou par des déductions à partir de la définition avancée.

H2a: Le Postulat d'Eudoxe-Archimede se trouve dans ce cas. (Il est clairement identifiable à l'un des langages ou il intervient) (Chapitre 7)
 

b) D'autres hypothéses vont pouvoir etre éprouvées expérimentalement:

H2b: Le Postulat d'Eudoxe-Archimede est une connaissance pour certains élevés. Il produit des réponses adaptées dans un certain contexte fréquemment rencontré. (Le contexte fréquemment rencontré est lié aux conceptions spontanées).

H2c1: Dans un contexte non-Archimedien, la connaissance du Postulat d'Eudoxe-Archimede se manifeste par des erreurs assez nombreuses.

H2c2: Quand on généralise le contexte, le Postulat d'Eudoxe-Archimede continue à se manifester.
Quand on a pris en considération un contexte général des Grandeurs ou l'Archimedeicité ou la non-Archimedeicité sont des cas particuliers, le Postulat se manifeste comme obstacle.

H2d: Le Postulat d'Eudoxe-Archimede résiste aux contradictions auxquelles il est confrontée. Dans un contexte plus général, le P.E.A. ne sera pas réorganisée (et acceptée) aprés avoir produit des contradictions par rapport aux connaissances déjà acceptées par l'éléve.

H2e: Le Postulat d'Eudoxe-Archimede continue à se manifester aussi aprés sa prise de conscience.
C'est-à-dire que, aprés avoir pris conscience du role du P.E.A. dans le nouveau langage, demeurent les conceptions relatives au role du P.E.A. du langage du départ.

11.6 - Démontrer que le Postulat d'Eudoxe-Archiméde est un Obstacle épistémologique

On reprend le Modèle sur l'obstacle épistémologique et nous voyons de vérifier les hypothèses qui concernent le Postulat d'Eudoxe-Archiméde.

L'hypothèse H1 a étè pleinement discutée dans le chapitre sur l'histoire et l'épistémologie (Chapitre 7). Le Postulat d'Eudoxe-Archiméde est un des éléments constitutifs de quelques langages mathématiques. Le Tableau du chapitre 7 (7.3) le montre.

L'hypothèse H2a a étè aussi discutée dans le chapitre 7 sur l'histoire et l'épistémologie. Le Postulat d'Eudoxe-Archiméde est une connaissance clairement identifiable dans chacun des langages dans lesquels il intervient.

11.7 Les manifestations prévues suivant les hypothèses

En ce qui concerne la partie expérimentale il faut prendre en considération les questions groupées suivantes qui représentent la maniére d'argumenter les hypothèse H2b, H2c1, H2c2 H2d, H2e:

En particulier les questions 1a1 2a1, sur la définition du Postulat d'Eudoxe-Archiméde, ne sont pas Réussit/échec. Dans l'analyse factorielle qui sera présentée aprés elles, ne sont pas pris en considération .

11.8 Résume des questions et des variables de comportement.

11.9. Les variables de la situation

Les valeurs des variables cognitives et didactiques (toutes binaires) de la situation de base doivent faire apparaetre que certains élèves connaissent et utilisent les P.E.A. sous diverses formes (explicitement, implicitement...) et dans certaines circonstances, à tort ou à raison.
Le tableau suivant résume les variables oppositives retenues pour l'expérience.

11.10. Le plan d'expérience. Matrice explicative. Mèthode.

Le croisement complet de toutes les variables n'était pas logiquement possible mais nous avons retenu finalement 22 questions réparties en un plan d'expérience disposé comme suit.

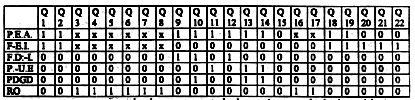
Ces questions sont l'occasion de comportements de réponses (par exemple réussite ou échec). Les comportements de réponses caractéristiques des hypothèses étudiées doivent etre déterminés a priori. Cette description prend la forme d'un ensemble de "variables de comportements" qui détermine les observables.
Nous avons finalement retenu 24 variables de comportements dont les valeurs pour chaque élève observé constitueront la matrice de contingence (matrice des observation).
Chaque variable de comportement est ainsi elle meme repérée par rapport aux situations dans lesquelles elle est recueillie, par une matrice explicative des questions (ou observations supplémentaires) qui peut etre confrontée aux résultats des analyses de données. Chaque ligne de cette matrice peut s'interpréter comme représentant un profil caractéristique possible des élèves.

De cette manière il est possible d'examiner l'effet sur les comportements des variables étudiées et d'en tirer des conclusions sur les hypothèses mises à l'épreuve.

11.11 Analyses et Résultats
11.11.1. Analyse des fréquences de réussite

    Tableau des comportement de réussite

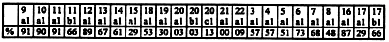
H2é
Nous allons d'abord confronter ces résultats marginaux avec les hypothèses étudiées au moyen de tests élémentaires: Nous accepterons qu'un pourcentage de réussite qui s'écarte significativement de 50% manifeste soit une connaissance, soit une ignorance, dans la population considérée.
Les questions manifestant la connaissance du P.E.A. dans le cas numérique
- direct sont: {1a1; 9a1; 10a1; 11a1} 90 % de réussite
- inverse sont: {2a1; 12a1; 13a1; 14a1} 70% de réussite,
sur l'ensemble, 80 % qui différe significativement de 50%
de plus la différence de pourcentage entre les deux conditions est significative.
Conclusion: l'Hypothèse H2b ne peut etre rejetée, nous choisissons de l'admettre: les élèves utilisent le Postulat d'Eudoxe-Archiméde dans les cas ou il est réalisé et mieux dans le sens direct qu'inverse.
Peut etre y a-t-il dans la formulation de l'inverse, des problèmes de formalisation linguistique? Ces problèmes se sont déjà présentés dans l'histoire. La formulation inverse parait plus tard que la directe, avec PASCAL en 1600.

L'hypothèse H2c1 affirme que lors d'un changement de contexte les éléves continuent à appliquer la connaissance ancienne alors qu'elle n'est plus réalisée. Ce comportement se manifeste expérimentalement par une réponse fausse aux variables suivantes.
{15a1; 18a1; 19a1} {29%; 53 %; 30%} 34% de réussite
Le changement de point de vue fait baisser considérablement le pourcentage des réponses correctes. Il reste cependant encore élevé et ceci est lié au fait que le changement de point de vue porte sur la formulation directe du Postulat (la conception plus solide).
H2c2
L'hypothèse H2c2 qui concerne la généralisation ne repose que sur les réponses à la question 20a1. Il y est demandé de vérifier la proposition X,1 dans un contexte des Grandeurs Non-Archimédiennes. Pour pouvoir résoudre cette question, il faudrait pouvoir revoir les Grandeurs Archimédiennes et Non-Archimédiennes comme classe des Grandeurs homogénes. Le pourcentage des réponses correctes est de 1.3%. Ce résultat signifie que la généralisation ne s'est pas produite.
H2d
L'hypothèse H2d énonce que les élèves conservent l'hypothèse du PEA malgré qu'elle soit contredite par les faits auxquels elle est confrontée. Elle serait contredite par des taux élevés de réussites aux questions 20b1 et 20c1. (confrontation d'un angle de contingence et rectiligne). Il évoque l'information, connue par tous les élèves, que la droite tangente à un cercle en un point est unique.
Le pourcentages de réussite aux deux questions sont <1%.
H2e
L'hypothèse H2e, relative à la persistance de la connaissance/obstacle est éprouvée dans les questions 21a1 et 22a1. Les deux questions reprennent la problèmatique de la question 20a1, comme prise de conscience du problème; mais les élèves ne réussissent pas à comparer significativement leurs modèles interprétatives avec le contexte généralisé. La pourcentage des réponses à la question 18a1 (relation entre angle de contingence et rayon) a étè de 53.3% ce qui prouve que les *l*ves ont pris en charge le problème.
Les pourcentages de deux questions sont <1% avec un *cart <0.3.
Aucune des comparaisons de pourcentages ne contredit les hypothèses du Modèle concernant l'obstacle épistémologique.
 

11.11.2 Analyses des données

a) Enjeux
Il s'agit maintenant de savoir
-dans quelle mesure les résultats qui apparaissent sur les marges sont confirmés et importants par rapport aux autres sources de dispersion. Les variables étudiées déterminent elles les axes principaux? Lesquelles sont liées entre elles, lesquelles sont indépendantes?
- peut-on identifier des groupements d'élèves qui se comportent suivant le meme profil et correspondant aux deux "conceptions": PEA domin* (généralisé) ou PEA/obstacle? Sinon, les valeurs marginales résulteront de comportements individuels incohérents (erratiques) mais fortement déterminés par les situations. L'obstacle ne sera pas une "connaissance des élèves" mais plutot une "difficulté liée aux situations et aux savoirs".
La situation des données est la suivante: Matrice de la contingence (matrice active): échantillon de 107 élèves et 24 variables, Matrice explicative de 5 variables supplémentaires, et matrice explicative de 2 profils d'élèves.
Variables suppl*mentaires: sommes des valeurs sur les variables caract*ristiques
FT Réussite des élèves (somme sur toutes les variables)
PAD Profil "Postulat d'Eudoxe-Archiméde (Direct)" somme 9a1, 10a1, 11a1, 11b1, 15a1
PAI Profil "Postulat d'E.-A. (Inverse)"
NPA Profil répond bien sur les "contextes non Archimédiens"
RO Profil sur la relation d'ordre
Les profils élèves sont:
So1 Profil obstacle épistémologique du P.d'E.-A.
So2 Profil sur la négation de So1.
b) Analyse en composante principale (ACP)

Les pourcentages d'inertie portés par les axes principaux sont :

Si chaque question était indépendante des autres et apportait la meme information, elle déterminerait 100/24= 4.1% de l'inertie totale. Les quatre premier axes sont significatifs.
Le premier plan principal (28% d'inertie) montre une assez forte auto corrélation des variables (toutes dans un angle de 120¡), facteur G qui exprime une tendance de certains élèves à avoir plus de réussites partout. L'axe des réussites générales est indiqué par FT, corrélé avec NPA.
Les seules variables qui s'expriment dans ce plan (contribution et corrélations importantes) sont:
- 5a1; 3a1 et 4a, elles déterminent l'axe 1 qui peut ainsi s'interpréter comme la réussite aux questions sur l'ordre (groupe de variables I) sur la figure 1 (page 133, Annexes);
- et 9a1 et 10a1 qui déterminent l'axe 2. lequel peut s'interpréter comme déterminé par la réussite aux questions ou le PEA direct doit etre acquis. Les questions ou le PEA doit etre accepté (groupe de variables II: 11a; 11b; 12a) sont partiellement corrélées dans ce plan.
Deux variables supplémentaires RO et PAD se placent bien sur les deux premiers axes principaux. (les autres variables supplémentaires:
L'examen de la distribution de la population dans le premier plan principal montre de facon assez nette une discrimination par une droite de grande pente (groupes d'élèves a et b) ce qui tendrait à montrer que les questions sur l'ordre sont plus discriminantes que les questions sur le PEA. Toutefois, les deux patrons SO1 (patron d'un élève qui utilise toujours le PEA meme lorsqu'il n'y a pas lieu et réussit aux questions d'ordre) et NSO1 (patron opposé) sont discriminés par l'axe 2 et se trouvent au milieu de deux paquets discriminés d'élèves: a1 et a2 (Figure 2, Annexes, page 134). { 003; 088, 013, 031, 037, 032 061 084, 071} et peut etre {007, 044, 024, 025, 041}qui pourraient ainsi déterminer deux conceptions.
Le deuxiéme plan principal montre un groupe de variable (Groupe III: 18a; 19a; 22a; 17a; 15a;) fortement corréme axe mais il ne détermine aucune discrimination observable. (Figure 3, Annexes, page 134-bis)
c) Analyse factorielle des correspondance (AFC)
L'analyse a étè effectuée avec le logiciel STATITCF du LADIST de Bordeaux.
On a utilisé l'analyse en composante principale (ACP) et l'analyse factorielle des correspondances simples (AFC).

L'analyse factorielle des correspondances permet-elle de mieux comprendre les rapports de la distribution des élèves avec les comportements aux questions?
comme toujours le facteur G disparait, FT est au centre. Presque tous les élèves se sont regroupés autour de cette variable. L'axe 1 semble déterminé par les variables 20a, 20b et 22a, l'axe 2 uniquement par la variable 21a. Tous les autres objets sont écrasés au centre. Il n'apparait nettement aucune discrimination ({059, 053, 016, 052, 103}
On observe que sur chacun des 5 axes, le profil So1 (obstacle) est placé prés du centre avec plus de 87.8% des élèves; le profil So2 (rejet de l'obstacle) est plus éloigné du centre mais ne regroupe pas autour de lui un groupe d'élèves. Cette conception n'existe pas ou peu.

Conclusion. Si le Postulat d'Eudoxe-Archiméde représente un obstacle épist*mologique parce que le "profil obstacle" So1 se détache de So2. seule la conception "usage universel du P.E.A." est susceptible d'etre observée (pourcentage d'élèves > 87.8% dans les 5 axes, 98% sur les deux premiers).

11.11.3 Analyse implicative

L'analyse a étè effectuée avec le logiciel CHIC du LADIST de Bordeaux mis au point par R. GRAS et alii du I.R.M.A.R. (Institut de Recherche Mathématique de Rennes).
On a utilise l'implication des variables, la construction de graphes implicatifs et la Hiérarchie implicative des classes. Il n'a pas étè possible de caractériser les individus ou/et les catégories déterminantes parce que CHIC n'accepte que des variables binaires.
L'*chantillon est le meme que celui de l'analyse factorielle : 24 variables et 107 élèves.
L'occurrence des variables suit le profil obstacle.
L'échantillon complet donne un graphe implicatif ou la variable 20c1 (Donner une justification au processus de vérification de la proposition X,1 sur un contexte non Archimédienne), qui est li*e à l'hypothèse H2d du Modèle d'obstacle épistémologique sur la Résistance aux contradictions, implique toutes les autres 23 variables.
Si on considére une nouvelle matrice ou la variable 20c1 n'existe pas, on trouve une condition de transitivité de presque toute, les autres variables ( la transitivité est vérifiée avec le seuil 0.50 d'implication). Mais on peut aussi affirmer que les variables sont indépendantes.
On peut dire que la résistance aux contradictions pourrait etre le noeud de l'obstacle épistémologique, comme cela a étè aussi vérifié dans l'histoire. En particulier, sur la Résistance aux contradictions la justification verbale sur une situation est plus forte que le procédé.
Tout changement d'orbite vers le noyau attracteur (20c1) peut témoigner que l'obstacle épistémologique peut etre caractérisé surtout par la Résistance aux contradictions.
Dans le Modèle on n'avait pas de hiérarchie, toutes les conditions devaient etre les memes.
Avec la Thèorie d'implication des classes on peut:
1- affirmer que les variables sont indépendants;
1- avancer l'hypothèse que la Résistance aux contradictions caractérise l'obstacle. Il faudrait encore des observations expérimentales pour permettre une meilleure argumentation.

11.12. Conclusions et perspectives

1. La caractérisation des obstacles en mathématiques, proposée par Duroux-Brousseau à partir des travaux de G.Bachelard, ne permet, au mieux, que de reconna etre qu'une connaissance est un obstacle, lorsqu'on à l'idée de s'interroger sur elle à ce sujet. Elle ne donne aucun moyen de chercher les obstacles a priori, elle ne fournit aucune clarification ni aucun indice de leur importance.
La tentative de définir des critéres qui ne seraient ni historiques ni didactiques pour identifier des obstacles de facon épistémologique nous a conduit à adopter une approche sémiotique des mathématiques. Identifier les obstacles épistémologiques par leurs caractéres syntaxiques dans les langages mathématiques donnerait beaucoup plus de chance et de facilités pour les trouver.
La théorie des situations avait mis l'accent sur le role des caractéres ergonomiques et informationnels dans leur genèse des connaissances et donc dans les processus didactiquesà
En utilisant ces deux cadres nous avons montré qu'un obstacle était lié à un caractére important du langage, lui meme associe à des modifications importantes de choix axiomatiques: Les obstacles doivent etre cherchés en premier lieu dans les changements de postulats, ces axiomes acceptés trop universellement et trop longtemps comme évidents et indispensables
D'autres investigations seraient toutefois n*cessaires pour confirmer la nature d'obstacle épistémologique des postulats et des systémes axiomatiques les plus répandus et inversement pour examiner si tous les obstacles identifiés à ce jour expérimentalement sont bien d'origine axiomatique.

2. Le Postulat d'Eudoxe-Archimede est une connaissance qui constitue une obstacle épistémologique à l'introduction préalable des hyper-réels et peut etre à la compréhension de l'analyse non standard.
Pour cette étude nous avons examiné deux nouvelles conditions qui étaient réalisées dans l'exemple choisi sur le changement de point de vue qui se produit qui avec le changement du contexte ou du langage et la généralisation qui se produit avec un élargissement du langage.

3. Ces nouvelles conditions sont elles contenues (logiquement et/ou sémantiquement) dans le modèle Duroux-Brousseau? ou en sont elles des conséquences? ou permettent elles une nouvelle classification des obstacles, faut il les adjoindre au modèle initial?
Il semble que les conditions nouvelles soient impliquées par le modèle de Duroux-Brousseau dans le sens que chaque obstacle déterminé avec le modèle Spagnolo-Duroux-Brousseau (par adjonction des deux conditions ci dessus) est un obstacle dans le sens du modèle Duroux-Brousseau.

4. Il y a encore beaucoup de travail à faire pour mieux comprendre le role du langage dans la modèlisation theorique-experimental pour l'individuation des obstacles épistémologiques: relation entre langage et point de vue; relation entre langage mathématique et changement de stratégie.
Le modèle theorique-experimental pour la recherche des obstacles épistémologiques donne la possibilité aux chercheurs en Didactique des mathématiques de vérifier sa validité, en certain circonstances, des obstacles épistémologiques.
De prochaines recherches théoriques et expérimentales pourront préciser les relations entre les deux modèles. On pourra aussi valider ce Modèle théorique-expérimental avec les autres modèles de recherche sur les obstacles épistémologiques déjà faits par des autres chercheurs en didactiques des mathématiques.