Involucri convessi (convex hull) per 3 eventi
Contents
- Eventi logicamente indipendenti
- Tre Eventi con una restrizione logica
- Tre Eventi con due restrizioni logiche
- Caso 1) I due vertici appartengono ad un lato del cubo
- Caso 2) I due vertici appartengono ad una diagonale di una faccia del cubo
- Caso 3) I due vertici appartengono ad una diagonale centrale del cubo
- Tre Eventi con tre restrizioni logiche
- Caso 1) I tre vertici appartengono ad una stessa faccia del cubo
- Caso 2) I tre vertici appartengono ad un piano che divide il cubo a metà
- Caso 3) Due vertici appartengono ad una diagonale di una faccia e il terzo appartiene alla diagonale perpendicolare della faccia opposta
- Tre Eventi con quattro restrizioni logiche
- Caso 1
- Caso 2
- Caso 3
- Caso 4
- Caso 5
- Caso 6
Eventi logicamente indipendenti
Consideriamo i tre eventi

Abbiamo la seguente matrice
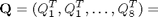
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
L'involucro convesso generato dagli 8 vertici è mostrato nella figura seguente

Tre Eventi con una restrizione logica
Ci sono
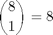
differenti vertici che possono essere eliminati da un cubo che rappresentano una restrizione logica.
Nell'esempio in questione non abbiamo il vertice

ovvero abbiamo la restrizione logica
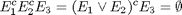
cioè
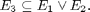
Abbiamo la seguente matrice
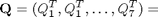
0 0 0 1 1 1 1
0 1 1 0 0 1 1
0 0 1 0 1 0 1
L'involucro convesso generato dai 7 vertici è mostrato nella figura seguente
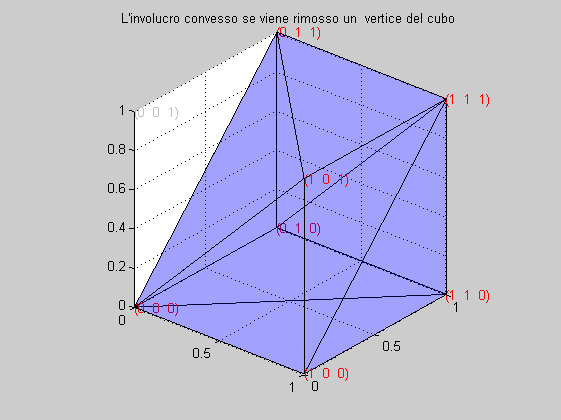
Tre Eventi con due restrizioni logiche
Ci sono
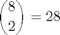
differenti modi nei quali due vertici possono essere eliminati da un cubo. Si hanno 3 casi
- 1) I due vertici appartengono ad un lato del cubo (12 lati)
- 2) I due vertici appartengono ad una diagonale di una faccia del cubo (12 diagonali facciali)
- 3) I due vertici appartengono ad una diagonale centrale del cubo (4 diagonali centrali)
Caso 1) I due vertici appartengono ad un lato del cubo
Non abbiamo i vertici
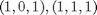
ovvero abbiamo la restrizioni logiche

cioè
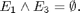
Abbiamo la seguente matrice
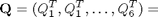
0 0 0 0 1 1
0 0 1 1 0 1
0 1 0 1 0 0
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente

Caso 2) I due vertici appartengono ad una diagonale di una faccia del cubo
Non abbiamo i vertici
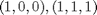
ovvero abbiamo la restrizioni logiche
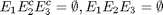
cioè

Ad esempio nel lancio di un dado gli eventi possono essere così definiti:

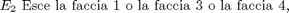

Abbiamo la seguente matrice
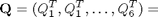
0 0 0 0 1 1
0 0 1 1 0 1
0 1 0 1 1 0
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente
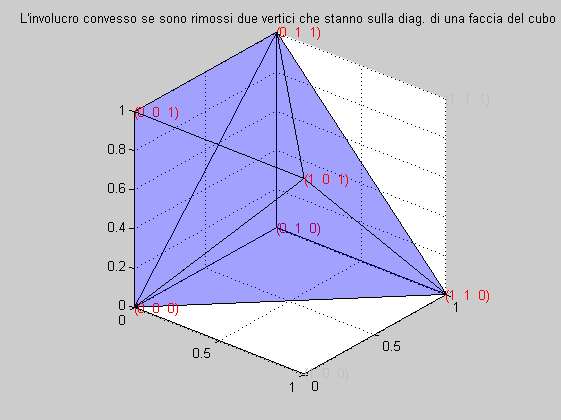
Caso 3) I due vertici appartengono ad una diagonale centrale del cubo
Non abbiamo i vertici
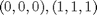
ovvero abbiamo la restrizioni logiche
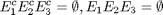
cioè, non possono essere tutti e tre veri o tutti e tre falsi.
Abbiamo la seguente matrice
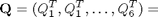
0 0 0 1 1 1
0 1 1 0 0 1
1 0 1 0 1 0
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente
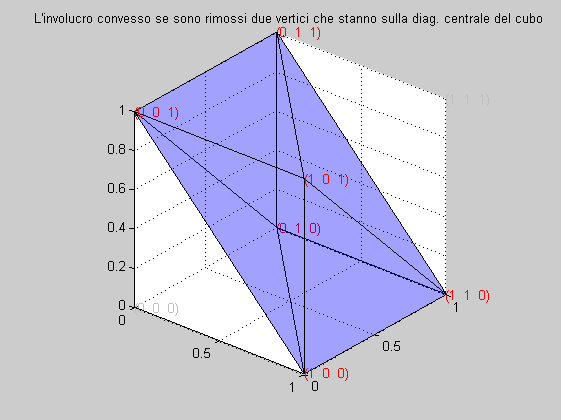
Tre Eventi con tre restrizioni logiche
Ci sono

differenti modi nei quali tre vertici possono essere eliminati da un cubo. Si hanno 3 casi
- 1) I tre vertici appartengono ad una stessa faccia del cubo (24)
- 2) I tre vertici appartengono ad un piano che divide il cubo a metà (24)
- 3) Due vertici appartengono ad una diagonale di una faccia e il terzo appartiene alla diagonale perpendicolare della faccia opposta (8)
Caso 1) I tre vertici appartengono ad una stessa faccia del cubo
Non abbiamo i vertici
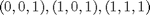
Abbiamo la seguente matrice
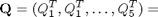
0 0 0 1 1
0 1 1 0 1
0 0 1 0 0
L'involucro convesso generato dai 5 vertici è mostrato nella figura seguente
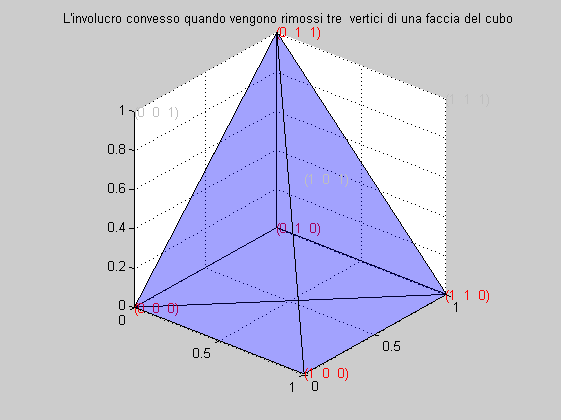
Caso 2) I tre vertici appartengono ad un piano che divide il cubo a metà
Non abbiamo i vertici
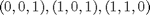
Abbiamo la seguente matrice
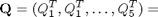
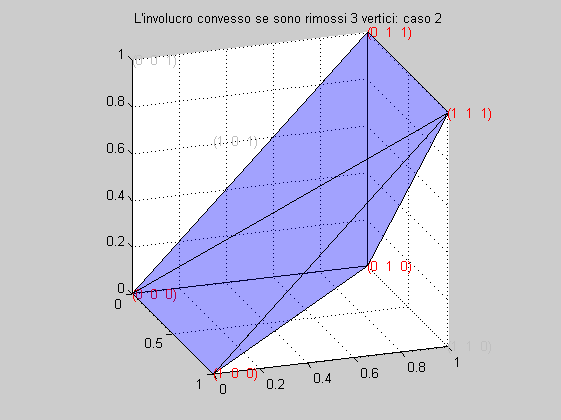
0 0 0 1 1
0 1 1 0 1
0 0 1 0 1
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente
Caso 3) Due vertici appartengono ad una diagonale di una faccia e il terzo appartiene alla diagonale perpendicolare della faccia opposta
Non abbiamo i vertici
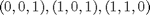
Abbiamo la seguente matrice
0 0 0 1 1
0 0 1 0 1
0 1 1 1 0
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente

Tre Eventi con quattro restrizioni logiche
Ci sono

differenti modi nei quali tre vertici possono essere eliminati da un cubo. Si hanno 6 casi
Caso 1
Abbiamo la seguente matrice
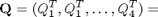
0 1 1 1
1 0 1 1
1 1 0 1
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente

Caso 2
Abbiamo la seguente matrice
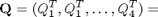
0 0 1 1
0 1 0 1
0 1 1 1
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente
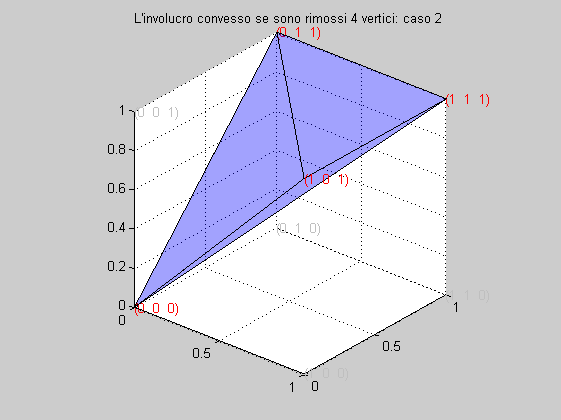
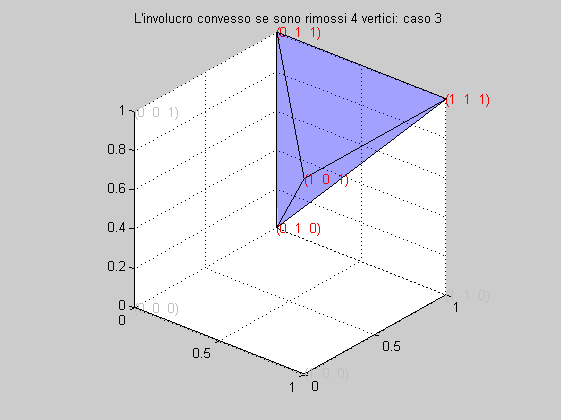
Caso 3
Abbiamo la seguente matrice
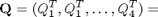
0 0 1 1
1 1 0 1
0 1 1 1
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente
Caso 4
Abbiamo la seguente matrice
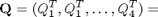
0 1 1 1
1 0 0 1
1 0 1 1
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente

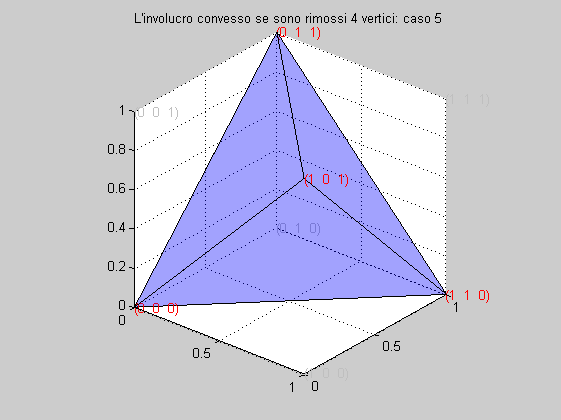
Caso 5
Abbiamo la seguente matrice
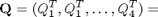
0 0 1 1
0 1 0 1
0 1 1 0
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente
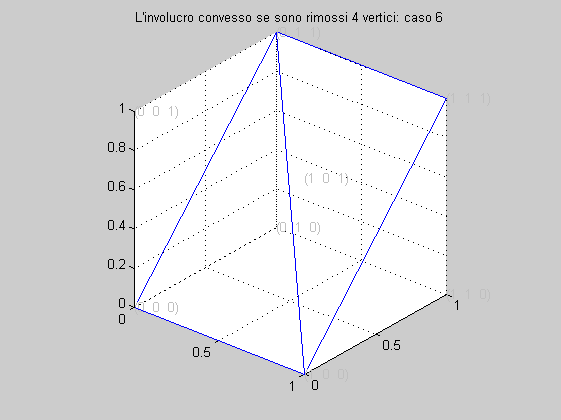
Caso 6
Abbiamo la seguente matrice
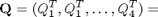
0 0 1 1
0 1 0 1
0 1 0 1
L'involucro convesso generato dai 6 vertici è mostrato nella figura seguente